
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)

【答案】(1) BC=8 m;(2)点D离地面的高为4.5 m.
【解析】
试题(1)根据坡度定义直接解答即可;
(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据![]() ,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
试题解析:(1)∵坡度为i=1:2,AC=4m,
∴BC=4×2=8m.
(2)作DS⊥BC,垂足为S,且与AB相交于H.

∵∠DGH=∠BSH,∠DHG=∠BHS,
∴∠GDH=∠SBH,
![]()
∵DG=EF=2m,
∴GH=1m,
∴DH=![]() m,BH=BF+FH=3.5+(2.5-1)=5m,
m,BH=BF+FH=3.5+(2.5-1)=5m,
设HS=xm,则BS=2xm,
∴x2+(2x)2=52,
∴x=![]() m,
m,
∴DS=![]() +
+![]() =2
=2![]() m≈4.5m.
m≈4.5m.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
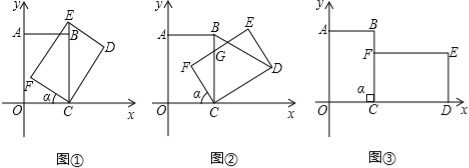
(1)如图①,当点E在射线CB上时,E点坐标为 ;
(2)当△CBD是等边三角形时,旋转角a的度数是 (a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定T(x,y)=![]() (其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
(其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
如:T(3,1)=![]() ,T(m,﹣2)=
,T(m,﹣2)=![]() .
.
(1)填空:T(4,﹣1)= (用含a,b的代数式表示);
(2)若T(﹣2,0)=﹣2且T(5,﹣1)=6.
①求a与b的值;
②若T(3m﹣10,m)=T(m,3m﹣10),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,秋千链子的长度为4 m,当秋千向两边摆动时,两边的最大摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为( )
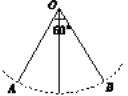
A. 2 m B. (4-![]() ) m C. (4-2
) m C. (4-2![]() ) m D. (4-2
) m D. (4-2![]() ) m
) m
查看答案和解析>>
科目:初中数学 来源: 题型:
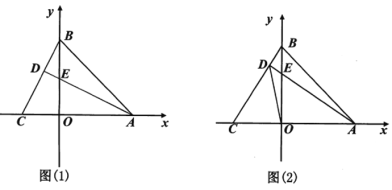
【题目】在平面直角坐标系中,点A(4,0),B(0,4),点C是x轴负半轴上的一动点,连接BC,过点A作直线BC的垂线,垂足为D,交y轴于点E.
(1)如图(1),
①判断![]() 与
与![]() 是否相等(直接写出结论,不需要证明).
是否相等(直接写出结论,不需要证明).
②若OC=2,求点E的坐标.
(2)如图(2),若OC<4,连接DO,求证:DO平分![]() .
.
(3)若OC>4时,请问(2)的结论是否成立?若成立,画出图形,并证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
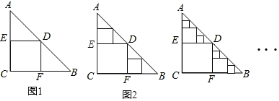
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板,![]() ,
,![]() ,在这张纸板中剪出一个尽可能大的正方形称为第
,在这张纸板中剪出一个尽可能大的正方形称为第![]() 次剪取;在余下的
次剪取;在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取(如图
次剪取(如图![]() );继续操作下去…;第
);继续操作下去…;第![]() 次剪取后,余下的所有小三角形的面积之和是________.
次剪取后,余下的所有小三角形的面积之和是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com