
【题目】对x,y定义一种新运算T,规定T(x,y)=![]() (其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
(其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
如:T(3,1)=![]() ,T(m,﹣2)=
,T(m,﹣2)=![]() .
.
(1)填空:T(4,﹣1)= (用含a,b的代数式表示);
(2)若T(﹣2,0)=﹣2且T(5,﹣1)=6.
①求a与b的值;
②若T(3m﹣10,m)=T(m,3m﹣10),求m的值.
【答案】(1)![]() ;(2)①a=1,b=-1,m=5.
;(2)①a=1,b=-1,m=5.
【解析】
(1)根据题目中的新运算法则计算即可;
(2)①根据题意列出方程组即可求出a,b的值;
②先分别算出T(3m﹣10,m)与T(m,3m﹣10)的值,再根据求出的值列出等式即可得出结论.
解:(1)T(4,﹣1)=![]()
=![]() ;
;
故答案为:![]() ;
;
(2)①∵T(﹣2,0)=﹣2且T(5,﹣1)=6,
∴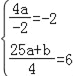
解得![]()
②解法一:
∵a=1,b=﹣1,且x+y≠0,
∴T(x,y)=![]() =
=![]() =x﹣y.
=x﹣y.
∴T(3m﹣10,m)=3m﹣10﹣m=2m﹣10,
T(m,3m﹣10)=m﹣3m+10=﹣2m+10.
∵T(3m﹣10,m)=T(m,3m﹣10),
∴2m﹣10=﹣2m+10,
解得,m=5.
解法二:由解法①可得T(x,y)=x﹣y,
当T(x,y)=T(y,x)时,
x﹣y=y﹣x,
∴x=y.
∵T(3m﹣10,m)=T(m,3m﹣10),
∴3m﹣10=m,
∴m=5.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米.他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶( )
.小王用自驾车方式上班平均每小时行驶( )
A. 26千米 B. 27千米 C. 28千米 D. 30千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G. 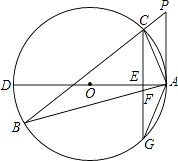
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ![]() ,AB=4
,AB=4 ![]() ,求△AFG的面积.
,求△AFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=5,AB=6,将它沿AB翻折得到△ABD,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是________.
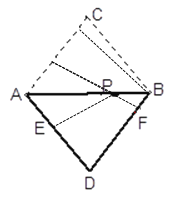
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.乙骑自行车的速度是( )米/分.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.乙骑自行车的速度是( )米/分.
A. 600 B. 400 C. 300 D. 150
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com