
【题目】小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米.他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶( )
.小王用自驾车方式上班平均每小时行驶( )
A. 26千米 B. 27千米 C. 28千米 D. 30千米
【答案】B
【解析】
设小王用自驾车方式上班平均每小时行驶x千米,根据已知小王家距上班地点18千米.他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() ,可列方程求解.
,可列方程求解.
∵小王家距上班地点18千米,
∴小王从家到上班地点所需时间t=![]() 小时;
小时;
∵他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,
∴他乘公交车从家到上班地点所需时间t=![]() ,
,
∵乘公交车方式所用时间是自驾车方式所用时间的![]() ,
,
∴![]() =
=![]() ×
×![]() ,
,
解得x=27,
经检验x=27是原方程的解,且符合题意.
即:小王用自驾车方式上班平均每小时行驶27千米.
故答案选:B.


科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
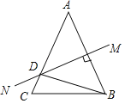
A. 50° B. 45° C. 55° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
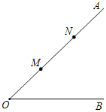
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定T(x,y)=![]() (其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
(其中a,b是非零常数,且x+y≠0),这里等式右边是通常的四则运算.
如:T(3,1)=![]() ,T(m,﹣2)=
,T(m,﹣2)=![]() .
.
(1)填空:T(4,﹣1)= (用含a,b的代数式表示);
(2)若T(﹣2,0)=﹣2且T(5,﹣1)=6.
①求a与b的值;
②若T(3m﹣10,m)=T(m,3m﹣10),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,之间的距离为2 ,
,之间的距离为2 , ![]() ,
,![]() 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD= ![]() AE2;④S△ABC=4S△ADF . 其中正确的有( )
AE2;④S△ABC=4S△ADF . 其中正确的有( ) 
A.1个
B.2 个
C.3 个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com