
【题目】以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是 .
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】在对全市初中生的体质健康测试中,青少年体质研究中心随机抽取的10名女生的立定跳远的成绩(单位:厘米)如下:123,191,216,191,159,206,191,210,186,227.
(1)通过计算,样本数据(10名女生的成绩)的平均数是190厘米,中位数是多少厘米?众数是多少厘米?
(2)本市一初中女生的成绩是194厘米,你认为她的成绩如何?说明理由;
(3)研究中心分别确定了一个标准成绩,等于或大于这个成绩的女学生该项素质分别被评定为“合格”、“优秀”等级,其中合格的标准为大多数女生能达到,“优秀”的标准为全市有一半左右的学生能够达到,你认为标准成绩分别定为多少?说明理由;按拟定的合格标准,估计该市4650人中有多少人在合格以上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米.他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶( )
.小王用自驾车方式上班平均每小时行驶( )
A. 26千米 B. 27千米 C. 28千米 D. 30千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=5,AB=6,将它沿AB翻折得到△ABD,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是________.
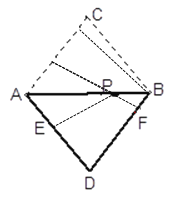
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论: ①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2 ,
其中正确的结论有( )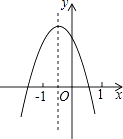
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE. 
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为___________.
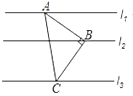
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE. 
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com