
【题目】在对全市初中生的体质健康测试中,青少年体质研究中心随机抽取的10名女生的立定跳远的成绩(单位:厘米)如下:123,191,216,191,159,206,191,210,186,227.
(1)通过计算,样本数据(10名女生的成绩)的平均数是190厘米,中位数是多少厘米?众数是多少厘米?
(2)本市一初中女生的成绩是194厘米,你认为她的成绩如何?说明理由;
(3)研究中心分别确定了一个标准成绩,等于或大于这个成绩的女学生该项素质分别被评定为“合格”、“优秀”等级,其中合格的标准为大多数女生能达到,“优秀”的标准为全市有一半左右的学生能够达到,你认为标准成绩分别定为多少?说明理由;按拟定的合格标准,估计该市4650人中有多少人在合格以上?
【答案】(1)中位数是:191,众数是191;(2)他的成绩比全市学生的平均成绩好;(3)标准成绩定为200厘米,3255.
【解析】
试题分析:(1)利用中位数和众数的定义即可求解,(2)可以从中位数和这组数据的平均数方面对这位学生成绩进行评价,(3)用这组数据的中位数作为一个标准衡量学生达到合格及优秀等级.
试题解析:(1)从小到大123,159,186,191,191,191,206,210,216,227,
所以中位数是:191,众数是191.
(2)根据(1)中得到的样本数据的结论,可以估计,在这次立定跳远的成绩测试中,全市学生的平均成绩是190厘米,这位学生的成绩是194厘米,大于平均成绩190厘米,可以推测他的成绩比全市学生的平均成绩好.
(3)如果合格的标准为大多数女生能达到,标准成绩应定为191厘米(中位数).因为从样本情况看,成绩在191厘米以上(含191厘米)的学生占总人数的大多数,全市有一半左右的学生评定为“优秀”等级,可以估计,如果标准成绩定为200厘米,全市将有一半左右的学生能够评定为“优秀”等级,
估计该市4650人中在合格以上的人数为:4650×![]() =3255(人).
=3255(人).


科目:初中数学 来源: 题型:
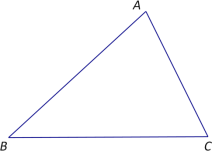
【题目】如图,已知△ABC,利用尺规,根据下列要求作图(保留作图痕迹,不写作法),并根据要求填空:
(1)作∠ABC的平分线BD交AC于点D;
(2)作BD的垂直平分线交AB于E,交BC于F;
(3)在(1)、(2)条件下,连接DE,线段DE与线段BF的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
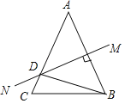
A. 50° B. 45° C. 55° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )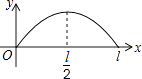
A.
B.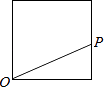
C.
D.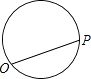
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班毕业联欢会设计的即兴表演节目的摸球游戏,游戏采用一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其它完全相同,游戏规则是参加联欢会的50名同学,每人将盒子乒乓球摇匀后闭上眼睛从中随机一次摸出两个球(每位同学必须且只能摸一次).若两球上的数字之和是偶数就给大家即兴表演一个节目;否则,下个同学接着做摸球游戏,依次进行.
(1)用列表法或画树状图法求参加联欢会同学表演即兴节目的概率;
(2)估计本次联欢会上有多少个同学表演即兴节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
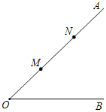
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com