
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
【答案】
(1)y=﹣x2+2x+3
(2)
解:令PP′交DE于G,
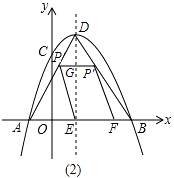
∵PP′∥AF,PE∥FP′,
∴四边形FEP′P是平行四边形,
∴PP′=EF,
∴△DPP′∽△DAB,
∴ ![]() ,
,
又∵A(﹣1,0)、B(3,0)、D(1,4),EF=x,
∴AB=4,DE=4,PP′=x,
∴ ![]()
∴GE=4﹣x,
又∵S四边形EPP'F=EFGE,
∴y=x(4﹣x)
∴y=x(4﹣x)=﹣(x﹣2)2+4,x=2时,y的最大值是4
(3)
解:假设存在满足条件的点Q(x,y),
作OH⊥BC于H,
∵Rt△BCQ中BC是直角边,
∴Rt△BCQ的另一直角边与OH平行.
又∵OC=OB,CO⊥OB,OB=3,OC=3,
∴Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到(如图).
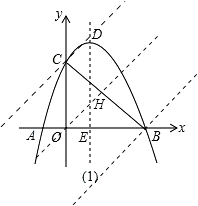
由已知得直线OH的解析式是y=x,
∴Rt△BCQ的另一直角边所在的直线解析式是:y=x+3或 y=x﹣3
点Q为直线y=x+3和抛物线交点,
则 ![]() ,
,
解得:x=1,
∴y=4;
②点Q为直线y=x﹣3和抛物线交点,
则 ![]() ,
,
解得:x=﹣2,
∴y=﹣5,
∴存在满足条件的点Q的坐标是:(1,4)和(﹣2,﹣5)
【解析】解:(1)∵抛物线y=ax2+bx+c(a≠0)经过点C,
则c=3,
∵抛物线经过A,B两点,∴ ![]()
解得:a=﹣1,b=2,
所以答案是 y=﹣x2+2x+3;
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,![]() ≈1.7,
≈1.7,![]() ≈1.4 ).
≈1.4 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm. 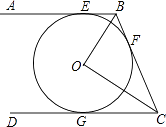
(1)求证:BO⊥CO;
(2)求BE和CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对全市初中生的体质健康测试中,青少年体质研究中心随机抽取的10名女生的立定跳远的成绩(单位:厘米)如下:123,191,216,191,159,206,191,210,186,227.
(1)通过计算,样本数据(10名女生的成绩)的平均数是190厘米,中位数是多少厘米?众数是多少厘米?
(2)本市一初中女生的成绩是194厘米,你认为她的成绩如何?说明理由;
(3)研究中心分别确定了一个标准成绩,等于或大于这个成绩的女学生该项素质分别被评定为“合格”、“优秀”等级,其中合格的标准为大多数女生能达到,“优秀”的标准为全市有一半左右的学生能够达到,你认为标准成绩分别定为多少?说明理由;按拟定的合格标准,估计该市4650人中有多少人在合格以上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 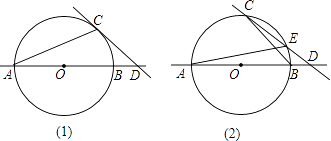
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米.他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶( )
.小王用自驾车方式上班平均每小时行驶( )
A. 26千米 B. 27千米 C. 28千米 D. 30千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE. 
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com