
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm. 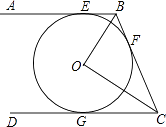
(1)求证:BO⊥CO;
(2)求BE和CG的长.
【答案】
(1)证明:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵AB、BC、CD分别与⊙O相切于E、F、G,
∴BO平分∠ABC,CO平分∠DCB,
∴∠OBC= ![]() ,∠OCB=
,∠OCB= ![]() ,
,
∴∠OBC+∠OCB= ![]() (∠ABC+∠DCB)=
(∠ABC+∠DCB)= ![]() ×180°=90°,
×180°=90°,
∴∠BOC=90°,
∴BO⊥CO
(2)解:连接OF,则OF⊥BC,
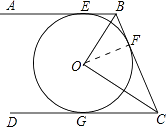
∴Rt△BOF∽Rt△BCO,
∴ ![]() =
= ![]() ,
,
∵在Rt△BOC中,BO=6cm,CO=8cm,
∴BC= ![]() =10cm,
=10cm,
∴ ![]() =
= ![]() ,
,
∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,
∴BE=BF=3.6cm,CG=CF,
∵CF=BC﹣BF=10﹣3.6=6.4cm.
∴CG=CF=6.4cm.
【解析】(1)由AB∥CD得出∠ABC+∠BCD=180°,根据切线长定理得出OB、OC平分∠EBF和∠BCG,也就得出了∠OBC+∠OCB= ![]() (∠ABC+∠DCB)=
(∠ABC+∠DCB)= ![]() ×180°=90°.从而证得∠BOC是个直角,从而得出BO⊥CO;(2)根据勾股定理求得AB=10cm,根据Rt△BOF∽Rt△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.
×180°=90°.从而证得∠BOC是个直角,从而得出BO⊥CO;(2)根据勾股定理求得AB=10cm,根据Rt△BOF∽Rt△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是

A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
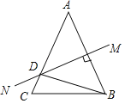
A. 50° B. 45° C. 55° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)计算:( ![]() ﹣2)0+(﹣1)2014+
﹣2)0+(﹣1)2014+ ![]() ﹣sin45°;
﹣sin45°;
(2)先化简,再求值:(a2b+ab)÷ ![]() ,其中a=
,其中a= ![]() +1,b=
+1,b= ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )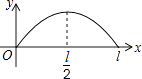
A.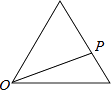
B.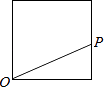
C.
D.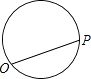
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,之间的距离为2 ,
,之间的距离为2 , ![]() ,
,![]() 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com