练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

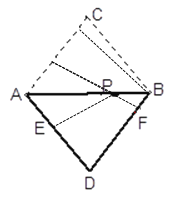
    【题目】如图，在△ABC中，AC=BC=5，AB=6,将它沿AB翻折得到△ABD，点P、E、F分别为线段AB、AD、DB的任意点，则PE+PF的最小值是________．

    【答案】

    【解析】

    根据题意证明四边相等即可得出菱形；作E关于AB的对称点E' ，连接E'F交AB于点P，交ABA于点P, 当E'F是AC，BD之间的距离时，E'F为最小.过点B作BH⊥AC于点H，求出BH的长即可.

    ∵AD=BD=AC= BC，∴四边形ADBC是菱形；

    如解图,作E关于AB的对称点E' ，根据菱形的对称性可知点E'在AC上，连接E'F交AB于点P，PE+PF=PE' +PF=E'F,当E'F是AC，BD之间的距离时，E'F为最小.过点B作BH⊥AC于点H，设AH=x，则CH=5 -x，由AB2－AH2 =BH2=BC2－CH2，得62 –x2 =25－(5－x)2，解得x＝，∴BH =，PE + PF的最小值为.故答案为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点间的距离y与点P走过的路程x的函数关系如图，那么点P所走的图形是（ ）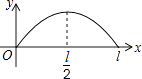

    A.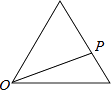
    B.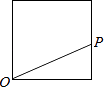
    C.
    D.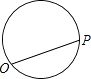

    查看答案和解析>>

    科目：初中数学 来源： 题型：

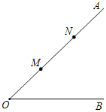
    【题目】如图，∠AOB=45°，点M，N在边OA上，OM=3，ON=7，点P是直线OB上的点，要使点P，M，N构成等腰三角形的点P有________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对x，y定义一种新运算T，规定T（x，y）=（其中a，b是非零常数，且x+y≠0），这里等式右边是通常的四则运算．

    如：T（3，1）=，T（m，﹣2）=．

    （1）填空：T（4，﹣1）=　 　（用含a，b的代数式表示）；

    （2）若T（﹣2，0）=﹣2且T（5，﹣1）=6．

    ①求a与b的值；

    ②若T（3m﹣10，m）=T（m，3m﹣10），求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，∠ABC＝90°,AB＝BC，三角形的顶点在相互平行的三条直线、、上，且,，之间的距离为2 , ,之间的距离为3 ,则AC2= _______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点．

    （1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；

    （2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE=AF吗？请利用图②说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以边长为2的正方形的中心O为端点，引两条相互垂直的射线，分别与正方形的边交于A、B两点，则线段AB的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx﹣3a（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），连接BC．

    （1）求该抛物线的解析式和对称轴，并写出线段BC的中点坐标；
    （2）将线段BC先向左平移2个单位长度，再向下平移m个单位长度，使点C的对应点C1恰好落在该抛物线上，求此时点C1的坐标和m的值；
    （3）若点P是该抛物线上的动点，点Q是该抛物线对称轴上的动点，当以P，Q，B，C四点为顶点的四边形是平行四边形时，求此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在锐角三角形ABC中，直线l为BC的中垂线，射线m为∠ABC的角平分线，直线l与m相交于点P.若∠BAC＝60°，∠ACP＝24°，则∠ABP的度数是( )

    A. 24° B. 30° C. 32° D. 36°

    查看答案和解析>>

    同步练习册答案