
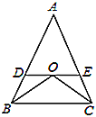
����Ŀ���ѱ߳��ֱ�Ϊ4��6�ľ���ABCO��ͼ����ƽ��ֱ������ϵ�У������Ƶ�C˳ʱ����תa�ǣ���ת��ľ��μ�Ϊ����EDCF������ת�����У�
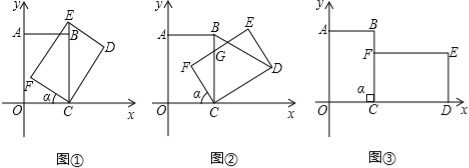
��1����ͼ��������E������CB��ʱ��E������Ϊ ��
��2������CBD�ǵȱ�������ʱ����ת��a�Ķ����� ��aΪ���ʱ����
��3����ͼ������EF��BC���ڵ�G����EG=CGʱ�����G�����ꣻ
��4����ͼ��������ת��a=90��ʱ�����жϾ���EDCF�ĶԳ�����H�Ƿ�����CΪ���㣬�Ҿ�����A���������ϣ�
���𰸡���1��E��4��2![]() ����
����
��2��60����
��3��![]() ��
��
��4����H���ڴ��������ϣ�
��������
���⣨1��������õ�E������CB�ϣ�������Ϊ4����������ݹ��ɶ����ɵõ�E��
��2����֪��BCD=60������BCF=30����Ȼ��ɵ��Ϧ�=60����
��3����CG=x����EG=x��FG=6��x�����ݹ��ɶ������CG��ֵ��
��4������CΪ����������ߵĽ���ʽΪy=a��x��4��2���ѵ�A������������aֵ����x=7ʱ���뺯������ʽ�ɵý⣮
�⣮��1��E��4��2![]() ��
��
��2��60��
��3����CG=x����EG=x��FG=6��x��
��Rt��FGC����CF2+FG2=CG2��
��42+��6��x��2=x2
���![]() ����
����![]()
��![]()
��4������CΪ����������ߵĽ���ʽΪy=a��x��4��2��
��A��0��6�����룬��6=a��0��4��2��
���a=![]() ��
��
�������ߵĽ���ʽΪy=![]() ��x��4��2
��x��4��2
������EDCF�ĶԳ�����H��Ϊ�Խ���FD��CE�Ľ��㣬
��H��7��2����
��x=7ʱ��![]()
����H���ڴ��������ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ�����
���ٶ��ƶ�����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����
�����![]() ��2
��2![]() ���ٶ��ƶ���
���ٶ��ƶ���
��1�������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ��������ô�����
ͬʱ��������ô�����![]() ���������6
���������6![]() ��
��
��2�������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ��������ô�����
ͬʱ��������ô�����![]() �ij��ȵ���7
�ij��ȵ���7![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
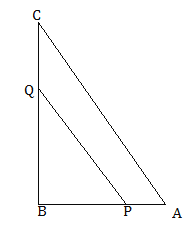
����Ŀ����ͼ���ڵ���![]() �У�
�У�![]() ��DΪBC���е㣬����C��
��DΪBC���е㣬����C��![]() �ڵ�G������B��
�ڵ�G������B��![]() �ڵ�B����CG���ӳ����ڵ�F������DF��AB�ڵ�E.
�ڵ�B����CG���ӳ����ڵ�F������DF��AB�ڵ�E.
(1)��֤��![]() ��
��
(2)��֤��AB��ֱƽ��DF��
(3)����AF�����ж�![]() ����״����˵������.
����״����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
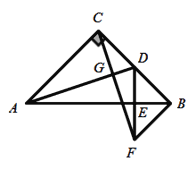
����Ŀ����ͼ����ABD����BDC��ƽ���߽���E��BE��CD�ڵ�F����1+��2=90������֤��

��1��AB��CD��
��2����2+��3=90����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=x2+bx+c�ĶԳ���Ϊx=2���ҹ���C��0��3��
��1����������ߵĽ���ʽ��
��2��֤�����������ߺ���ֱ��y=��2x+1�Ϸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
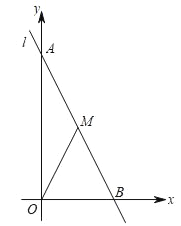
����Ŀ����ͼ����֪��ƽ��ֱ�������У�ֱ��l��y����2x+6�ֱ���������A��B���㣬M�Ǽ���AB��һ�����㣬���M�ĺ�����Ϊx����OMB�����ΪS��
��1��д��S��x�ĺ�����ϵʽ��
��2������OMB������ǡ�OAB�����![]() ʱ�����M�����ꣻ
ʱ�����M�����ꣻ
��3������OMB����OBΪ�ĵ��������Σ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() �У�
��![]() ��
��![]() ��
��![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ������
������![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ���ܳ�Ϊ18����
���ܳ�Ϊ18����![]() �ij���( )
�ij���( )
A.8B.9C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ִ�������һб��AB�����±�Ϊi��1��2������A���ĸ�ACΪ4 m��B��C��ͬһˮƽ���ϣ�
(1)��б��AB��ˮƽ����BC��
(2)����DEFGΪ�����λ���IJ���ͼ������DE��2.5 m��EF��2 m����������б���������ͣ���BF��3.5 mʱ�����D�����ĸߣ�(![]() ��2.236�������ȷ��0.1 m)
��2.236�������ȷ��0.1 m)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�DZ߳�Ϊ1��������ABCD�ĶԽ��ߣ�BEƽ�֡�DBC��DC�ڵ�E���ӳ�BC����F��ʹCF=CE������DF����BE���ӳ����ڵ�G.
��1����֤����BCE�ա�DCF��
��2����CF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com