
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
【答案】证明见解析
【解析】
试题分析:(1)首先根据角平分线的定义可得∠ABD=2∠1,∠BDC=2∠2,根据等量代换可得∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2),进而得到∠ABD+∠BDC=180°,然后根据同旁内角互补两直线平行可得答案;
(2)先根据三角形内角和定理得出∠BED=90°,再根据三角形外角的性质得出∠EDF+∠3=90°,由角平分线的定义可知∠2=∠EDF,代入得到∠2+∠3=90°.
证明:(1)∵DE平分∠BDC(已知),
∴∠ABD=2∠1( 角平分线的性质).
∵BE平分∠ABD(已知),
∴∠BDC=2∠2(角的平分线的定义).
∴∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2)( 等量代换).
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°( 等式的性质).
∴AB∥CD( 同旁内角互补两直线平行).
(2)∵∠1+∠2=90°,
∴∠BED=180°﹣(∠1+∠2)=90°,
∴∠BED=∠EDF+∠3=90°,
∵∠2=∠EDF,
∴∠2+∠3=90°.


科目:初中数学 来源: 题型:
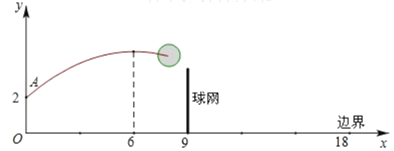
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2![]() 的A处发出,把球看成点,其运行的高度
的A处发出,把球看成点,其运行的高度![]() 与运行的水平距离
与运行的水平距离![]() 满足关系式
满足关系式![]() .已知球网与O点的水平距离为9
.已知球网与O点的水平距离为9![]() ,高度为2.43
,高度为2.43![]() ,球场的边界距O点的水平距离为18
,球场的边界距O点的水平距离为18![]() .
.
(1)当![]() =2.6时,求
=2.6时,求![]() 与
与![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(2)当![]() =2.6时,球能否越过球网?球会不会出界?请说明理由;
=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
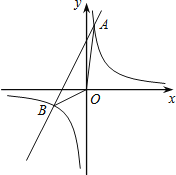
【题目】如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
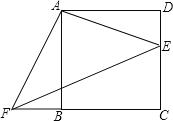
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一种内衣,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件的关系如表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)试求出y与x的之间的函数关系式;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价的什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)服装店决定将一周的销售内衣的利润全部捐给福利院,在服装店购进该内衣的贷款不超过8000元情况下,请求出该服装店最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,A、B、C、D四点共圆,过点C的切线CE∥BD,与AB的延长线交于点E.
(1)求证:∠BAC=∠CAD;
(2)如图②,若AB为⊙O的直径,AD=6,AB=10,求CE的长;
(3)在(2)的条件下,连接BC,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com