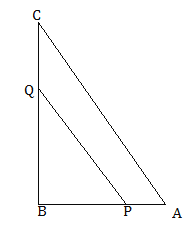
【题目】如图，在
中，
，
，
，点
从点
开始沿
边向点
以
的速度移动，点
从点开始沿
边向点
以2
的速度移动．
（1）如果点，分别从点，同时出发，那么几秒后，
的面积等于6
？
（2）如果点，分别从点，同时出发，那么几秒后，
的长度等于7
？
【答案】（1）出发1秒后，
的面积等于6
；（2）出发0秒或
秒后，
的长度等于7
．
【解析】
（1）设
秒后，的面积等于6，根据路程=速度×时间，即可用x表示出AP、BQ和BP的长，然后根据三角形的面积公式列一元二次方程，并解方程即可；
（2）设
秒后，的长度等于7，根据路程=速度×时间，即可用y表示出AP、BQ和BP的长，利用勾股定理列一元二次方程，并解方程即可．
解： （1）设秒后，的面积等于6，
∵点
从点
开始沿
边向点
以
的速度移动，点
从点开始沿
边向点
以2
的速度移动
∴
，
∴
则有
∴
（此时2×6=12＞BC，故舍去）
答：出发1秒后，的面积等于6
（2）设秒后，的长度等于7
∵点从点开始沿边向点以的速度移动，点从点开始沿边向点以2的速度移动
∴
，
∴
解得
答：出发0秒或秒后，的长度等于7．
科目：初中数学 来源： 题型：
【题目】随着智能手机的普及，微信抢红包已成为春节期间人们最喜欢的活动之一，某校七年级（1）班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．请根据以上信息回答：
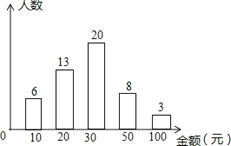
（1）该班同学所抢红包金额的众数是______，
中位数是______；
（2）该班同学所抢红包的平均金额是多少元？
（3）若该校共有18个班级，平均每班50人，请你估计该校学生春节期间所抢的红包总金额为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
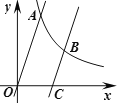
【题目】如图，反比例函数
（x＞0）的图象与一次函数y=3x的图象相交于点A，其横坐标为2．
（1）求k的值；
（2）点B为此反比例函数图象上一点，其纵坐标为3．过点B作CB∥OA，交x轴于点C，求点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
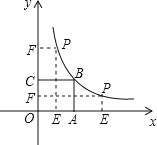
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=
（k>0,x>0）的图像上点P（m,n）是函数图像上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(1)求k的值；
(2)当S=
时 求p点的坐标；
(3)写出S关于m的关系式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：在坐标平面内，等腰直角
中，
，
，点
的坐标为
，点
的坐标为
，
交
轴于点
.
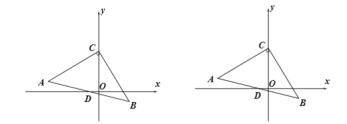
（1）求点
的坐标；
（2）求点的坐标；
（3）如图，点
在轴上，当
的周长最小时，求出点的坐标；
（4）在直线
上有点
，在轴上有点
，求出
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l1：
分别与x轴、y轴交于点B、C，且与直线l2：
交于点A．
（1）求出点A的坐标
（2）若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式
（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面方法，解答后面的问题：
（阅读理解）我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用。
例题：已知x可取任意实数，试求二次三项式
的取值范围。
解：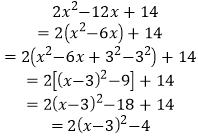
∵x取任何实数，总有
，∴
。
因此，无论x取任何实数，的值总是不小于-4的实数。
特别的，当x=3时，有最小值-4
（应用1）：已知x可取任何实数，则二次三项式
的最值情况是（ ）
A. 有最大值-10 B. 有最小值-10 C. 有最大值-7 D. 有最小值-7
（应用2）：某品牌服装进货价为每件50元，商家在销售中发现：当以每件90元销售时，平均每天可售出20件，为了扩大销售量，增加盈利，商家决定采取适当的降价措施。
（1）将市场调查发现：如果每件服装降价1元，那么平均每天那就可多售出2件，要想平均每天销售这种服装盈利为1200元，我们设降价x元，根据题意列方程得（ ）
A. 
B. 
C. 
D. 
（2）请利用上面（阅读理解）提供的方法解决下面问题：
这家服装专柜为了获得每天的最大盈利，每件服装需要降价多少元？每天的最大盈利又是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市为解决部分市民冬季集中取暖问题，需铺设一条长4000米的管道，为尽量减少施工对交通造成的影响，施工时“…”，设实际每天铺设管道x米，则可得方程
＝20，根据此情景，题中用“…”表示的缺失的条件应补为（ ）
A. 每天比原计划多铺设10米，结果延期20天完成
B. 每天比原计划少铺设10米，结果延期20天完成
C. 每天比原计划多铺设10米，结果提前20天完成
D. 每天比原计划少铺设10米，结果提前20天完成
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转a角，旋转后的矩形记为矩形EDCF．在旋转过程中，
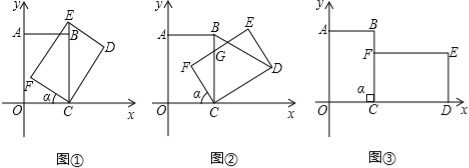
（1）如图①，当点E在射线CB上时，E点坐标为 ；
（2）当△CBD是等边三角形时，旋转角a的度数是 （a为锐角时）；
（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标；
（4）如图③，当旋转角a=90°时，请判断矩形EDCF的对称中心H是否在以C为顶点，且经过点A的抛物线上．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com