
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
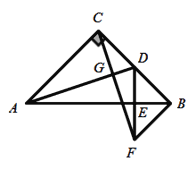
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)△ACF是等腰三角形,理由见解析.
【解析】
(1)先由CG⊥AD得到∠AGC=90°,证得∠CAD=∠FCB,再由AC=BC,FB⊥BC,根据“ASA”即可得出结论;
(2)由(1)△ACD≌△CBF,得出CD=BF,证得BD=BF,由△ABC是等腰直角三角形,得出∠DBE=45°,再证得∠DBE=∠FBE=45°,由“SAS”证出△DBE≌△FBE即可得出结论;
(3)由△CBF≌△ACD,得出CF=AD,由AB垂直平分DF,得出AF=AD,证得CF=AF,即可得出结论.
证明:(1)∵CG⊥AD,
∴∠AGC=90°,
∴∠GCA+∠CAD=90°,
∵∠GCA+∠FCB=90°,
∴∠CAD=∠FCB,
∵FB⊥BC,
∴∠CBF=90°,
∵Rt△ABC是等腰三角形,∠ACB=90°,
∴AC=BC,∠CBF=∠ACB,
在△ACD和△CBF中
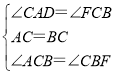 ,
,
∴△ACD≌△CBF(ASA);
(2)∵△ACD≌△CBF,
∴CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠DBE=45°,
∵∠CBF=90°,
∴∠DBE=∠FBE=45°,
在△DBE和△FBE中
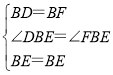 ,
,
∴△DBE≌△FBE(SAS),
∴DE=FE,∠DEB=∠FEB=90°,
∴AB垂直平分DF;
(3)△ACF是等腰三角形,理由为:
连接AF,如图所示,
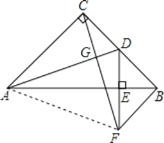
由(1)知:△CBF≌△ACD,
∴CF=AD,
由(2)知:AB垂直平分DF,
∴AF=AD,
∵CF=AD,
∴CF=AF,
∴△ACF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
![]() 求证:无论
求证:无论![]() 取任何实数时,方程总有实数根;
取任何实数时,方程总有实数根;
![]() 当抛物线
当抛物线![]() (
(![]() 为正整数)图象与
为正整数)图象与![]() 轴两个交点的横坐标均为整数,求此抛物线的解析式;
轴两个交点的横坐标均为整数,求此抛物线的解析式;
![]() 已知抛物线
已知抛物线![]() 恒过定点,求出定点坐标.
恒过定点,求出定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BD是对角线.分别过点A、C作AE⊥BD于点E,CF⊥BD于点F,且AE=CF

(1)求证:AB∥CD
(2)若E是BF中点,且△ABE的面积为1,则四边形ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为【 】

A.(4![]() +1.6)m B.(12
+1.6)m B.(12![]() +1.6)m C.(4
+1.6)m C.(4![]() +1.6)m D.4
+1.6)m D.4![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
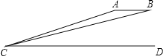
【题目】如图,某国侦察机![]() 飞抵我国近海搞侦察活动,我战斗机
飞抵我国近海搞侦察活动,我战斗机![]() 奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为
奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为![]() ,
,![]() ,它们与雷达的距离分别为
,它们与雷达的距离分别为![]() 千米,
千米,![]() 千米,求此时两机距离是多少千米?(精确到
千米,求此时两机距离是多少千米?(精确到![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB, OA上的动点,则△CDE周长的最小值是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣4,0),点B的坐标为(0,﹣2),把点A绕点B顺时针旋转90°得到的点C恰好在抛物线y=ax2上,点P是抛物线y=ax2上的一个动点(不与点O重合),把点P向下平移2个单位得到动点Q,则:
(1)直接写出AB所在直线的解析式、点C的坐标、a的值;
(2)连接OP、AQ,当OP+AQ获得最小值时,求这个最小值及此时点P的坐标;
(3)是否存在这样的点P,使得∠QPO=∠OBC,若不存在,请说明理由;若存在,请你直接写出此时P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
(1)若△CMN的周长为18cm,求AB的长.
(2)若∠MCN=48°,求∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com