
����Ŀ����ͼ����A������Ϊ����4��0������B������Ϊ��0����2�����ѵ�A�Ƶ�B˳ʱ����ת90���õ��ĵ�Cǡ����������y=ax2�ϣ���P��������y=ax2�ϵ�һ�����㣨�����O�غϣ����ѵ�P����ƽ��2����λ�õ�����Q����
��1��ֱ��д��AB����ֱ�ߵĽ���ʽ����C�����ꡢa��ֵ��
��2������OP��AQ����OP+AQ�����Сֵʱ���������Сֵ����ʱ��P�����ꣻ
��3���Ƿ���������ĵ�P��ʹ�á�QPO=��OBC���������ڣ���˵�����ɣ������ڣ�����ֱ��д����ʱP������꣮

���𰸡���1��a=![]() ����2��OP+AQ����СֵΪ2
����2��OP+AQ����СֵΪ2![]() ����ʱ��P������Ϊ����1��
����ʱ��P������Ϊ����1��![]() ������3��P����4��8����4��8����
������3��P����4��8����4��8����
��������
��1�����ô���ϵ�������ֱ��AB����ʽ��������ת����ȷ����C�����꣬������κ�������ʽ���a��ֵ���ɣ�
��2������BQ���ɵ�PQ��OBƽ�У���PQ=OB���õ��ı���PQBOΪƽ���ı��Σ���Q���߶�AB��ʱ�����OP+AQ����Сֵ���������ʱP�����꼴�ɣ�
��3�����������ĵ�P��ʹ�á�QPO=��OBC���籸��ͼ��ʾ���ӳ�PQ��x���ڵ�H�����ʱ��P������Ϊ��m��![]() m2�����������к�������ȷ����m��ֵ������ȷ����P�����꣮
m2�����������к�������ȷ����m��ֵ������ȷ����P�����꣮
��1����ֱ��AB����ʽΪy=kx+b��
��A����4��0����B��0����2������ã�![]() ��
��
��ã� ��
��
��ֱ��AB�Ľ���ʽΪy=��![]() x��2��
x��2��
��������ã���C������Ϊ��2��2����
��C��2��2��������κ�������ʽ�ã�a=![]() ��
��
��2������BQ��

����PQ��OB����PQ=OB��
���ı���PQBO��ƽ���ı��Σ�
��OP=BQ��
��OP+AQ=BQ+AQ��AB=2![]() �����Ⱥų����������ǵ�Q���߶�AB�ϣ���
�����Ⱥų����������ǵ�Q���߶�AB�ϣ���
��ֱ��AB�Ľ���ʽΪy=��![]() x��2��
x��2��
������ʱ��Q������Ϊ��t����![]() t��2����
t��2����
���ǣ���ʱ��P������Ϊ��t����![]() t����
t����
�ߵ�P��������y=![]() x2�ϣ�
x2�ϣ�
����![]() t=
t=![]() t2��
t2��
��ã�t=0��t=��1��
�൱t=0����P���O�غϣ��������⣬Ӧ��ȥ��
��OP+AQ����СֵΪ2![]() ����ʱ��P������Ϊ����1��
����ʱ��P������Ϊ����1��![]() ����
����
��3��P����4��8����4��8����
�籸��ͼ��ʾ���ӳ�PQ��x���ڵ�H��

���ʱ��P������Ϊ��m��![]() m2����
m2����
��tan��HPO=![]() ��
��
�֣���tan��OBC=![]() ��
��
��tan��HPO=tan��OBCʱ����ʹ�á�QPO=��OBC��
���ǣ���![]() ��
��
��ã�m=��4��
����P����4��8����4��8����


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AN��CB��B��N��ACͬ�࣬BM��CN���ڵ�D��AC��BC���ҡ�A+��MDN��180�㣮
��1����ͼ1������NAC��90�㣬��֤��BM��CN��
��2����ͼ2������NACΪ���ʱ�����ж�BM��CN��ϵ��֤����
��3����ͼ3���ڣ�1���������£��ҡ�MBC��30�㣬һ����E���߶�BM���˶������У���CE�����߶�CE�Ƶ�C˳ʱ����ת90����CF��ȡBE�е�P����AP��FP�����ı���APFC���ΪS����AM��![]() ��1��MC��1����E���˶������У���д��S��ȡֵ��Χ�� ����
��1��MC��1����E���˶������У���д��S��ȡֵ��Χ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣����ı���ABCD�У�AC��BD�ڵ�E��AB=AC=BD����MΪBC�е㣬NΪ�߶�AM�ϵĵ㣬��MB=MN.

��1����֤��BNƽ�֡�ABE��
��2����BD=1������DN�����ı���DNBCΪƽ���ı���ʱ�����߶�BC�ij���
��3����ͼ�ڣ�����FΪAB���е㣬����FN��FM����֤����MFN�ס�BDC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() �У�
�У�![]() ��DΪBC���е㣬����C��
��DΪBC���е㣬����C��![]() �ڵ�G������B��
�ڵ�G������B��![]() �ڵ�B����CG���ӳ����ڵ�F������DF��AB�ڵ�E.
�ڵ�B����CG���ӳ����ڵ�F������DF��AB�ڵ�E.
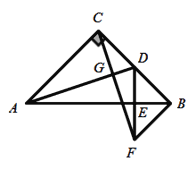
(1)��֤��![]() ��
��
(2)��֤��AB��ֱƽ��DF��
(3)����AF�����ж�![]() ����״����˵������.
����״����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ������һ�ִ��������һ�����������������4����ͬ��С�����Ϸֱ������0Ԫ������10Ԫ������20Ԫ������30Ԫ�����������涨���˿��ڱ��̳�ͬһ���ڣ�ÿ������200Ԫ���Ϳ������������Ⱥ�����������һ�������Żأ����̳�������С��������ĺͷ�����Ӧ�۸�Ĺ���ȯ�����������ڱ��̳����ѣ�ij�˿պ�����200Ԫ��
��1���ù˿����ٿɵõ�_____Ԫ����ȯ������ɵõ�_______Ԫ����ȯ��
��2�������û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����30Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ��
��![]() ��ͼ���ཻ�ڵ�
��ͼ���ཻ�ڵ�![]() ���ҵ�
���ҵ�![]() ��������Ϊ
��������Ϊ![]() �������
�������![]() �ķ���
�ķ���![]() �Ľ���________��
�Ľ���________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Թ�������ʵ������������Ĺ����о�������ѧ֪ʶ��һ������������������棬�������ܳ���![]() �������Ĵ�ϸ����������
�������Ĵ�ϸ����������![]() �ķ�������������ͼ����ͼ��ʾ��
�ķ�������������ͼ����ͼ��ʾ��

![]() �
�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
![]() ���������ܳ���Ϊ
���������ܳ���Ϊ![]() ��ʱ�������ĺ������Ƕ���
��ʱ�������ĺ������Ƕ���![]() ��
��
![]() ��Ҫ�������ĺ�����������
��Ҫ�������ĺ�����������![]() ʱ���������ܳ������Ϊ�����ף�
ʱ���������ܳ������Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C�ǡ�O��һ�㣬��P��ֱ��AB���ӳ����ϣ���O�İ뾶Ϊ3��PB=2��PC=4��
��1����֤��PC�ǡ�O�����ߣ�
��2����tan��CAB��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��DΪֱ��BC��һ���㣨�����B��C�غϣ�����AD���Ҳ�����ACE��ʹ��AE=AD����DAE=��BAC������CE��

��1����D���߶�![]() ��ʱ��
��ʱ��
����֤��![]() ��
��
�����жϵ�D�ںδ�ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
��2����![]() ʱ����
ʱ����![]() ����С��Ϊ28�㣬��
����С��Ϊ28�㣬��![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com