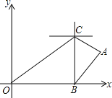
【题目】如图，已知点C（1，0），直线y=-x+7与两坐标轴分别交于A,B两点，D,E分别是AB, OA上的动点，则△CDE周长的最小值是_____________.
【答案】10
【解析】
点C关于OA的对称点C′（1，0），点C关于直线AB的对称点为C″，连接C′C″与AO交于点E，与AB交于点D，此时△CDE周长最小，这个最小值就是线段C′C″，然后求出C″的坐标即可解决问题．
解：如图，点C关于OA的对称点C′（1，0），点C关于直线AB的对称点C″，
∵直线AB的解析式为y＝x＋7，
∴设直线CC″的解析式为y＝x+b，
代入C（1，0）得：0=1+b，
解得：b=－1，
∴直线CC″的解析式为：y＝x1，
联立
，解得：
，
∴直线AB与直线CC″的交点坐标为K（4，3），
∵K是CC″中点，
∴C″（7，6），
连接C′C″与AO交于点E，与AB交于点D，此时△CDE周长最小，
△CDE的周长＝DE＋EC＋CD＝EC′＋ED＋DC″＝C′C″＝
，
故答案为：10．
科目：初中数学 来源： 题型：
【题目】如图，已知点
在
的
边上，
交
于
，
交
于
，若添加条件________，则四边形
是矩形；若添加条件________，则四边形是菱形；若添加条件________，则四边形是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在△ABC中，AB=AC，D是射线BC上一点(点D不与点B重合)，连结AD，将AD绕着点D逆时针旋转∠BAC的度数得到AE，连结DE、CE.
（1）当点D在边BC上，求证：△BAD≌△CAE.
（2）当点D在边BC上，若∠BAC=a，求∠DCE的大小．(用含a的代数式表示).
（3）当DE与△ABC的边所在的直线垂直，且∠BAC=40°时，请借助图②，直接写出∠CED的大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯．在雷达显示图上，标明了三艘海监船的坐标为
、
、
，（单位：海里）三艘海监船安装有相同的探测雷达，雷达的有效探测范围是半径为
的圆形区域（只考虑在海平面上的探测）．
若在三艘海监船组成的
区域内没有探测盲点，则雷达的有效探测半径至少为________海里；
某时刻海面上出现一艘菲律宾海警船
，在海监船
测得点位于南偏东
方向上，同时在海监船
测得位于北偏东
方向上，海警船正以每小时
海里的速度向正西方向移动，我海监船立刻向北偏东
方向运动进行拦截，问我海监船至少以多少速度才能在此方向上拦截到菲律宾海警船？
查看答案和解析>>
科目：初中数学 来源： 题型：
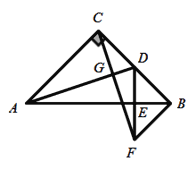
【题目】如图，在等腰
中，
，D为BC的中点，过点C作
于点G，过点B作
于点B，交CG的延长线于点F，连接DF交AB于点E.
(1)求证：
；
(2)求证：AB垂直平分DF；
(3)连接AF，试判断
的形状，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在7×7网格中，每个小正方形的边长都为1.
(1)若点A（1，3），C（2,1）， ①建立适当的平面直角坐标系；②点B的坐标为( ， );
(2)判断△ABC的形状，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰Rt△ABC中，∠BAC＝90°，AB＝AC,点A、点B分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E；
（1）如图（1），已知C点的横坐标为-1，直接写出点A的坐标；
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；
（3）如图（3）， 若点A在x轴上，且A（-4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连结CD交y轴于点P,问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
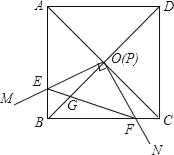
【题目】如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G．
（1）求四边形OEBF的面积；
（2）求证：OGBD=EF2；
（3）在旋转过程中，当△BEF与△COF的面积之和最大时，求AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
