
【题目】如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
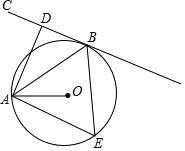
(1)求证:AB平分∠OAD;
(2)若点E是优弧 ![]() 上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
科目:初中数学 来源: 题型:
【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 于
于![]() ,
,![]() 于
于![]() ,并且
,并且![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 点向
点向![]() 点运动,动点
点运动,动点![]() 以
以![]() 的速度从点
的速度从点![]() 向点
向点![]() 运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为
运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为![]() .
.
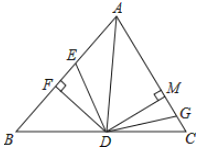
(1)求证:在运动过程中,不管![]() 取何值,都有
取何值,都有![]() ;
;
(2)当![]() 取何值时,
取何值时,![]() 与
与![]() 全等;
全等;
(3)若![]() ,当
,当![]() 时
时![]() ,求此时
,求此时![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)ABCD=![]() ;(4)∠ABE=∠DCE.
;(4)∠ABE=∠DCE.
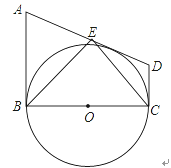
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
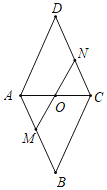
A. 28°B. 52°C. 62°D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,点点F作DE∥BC,交AB于点D,交AC于点E。若BD=3,DE=5,则线段EC的长为______.
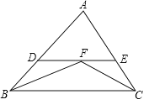
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形OABC是长方形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,已知长方形OABC的周长为16.
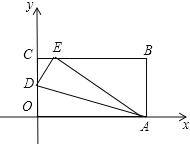
(1)若OA长为x,则B点坐标为_____;
(2)若A点坐标为(5,0),求点D和点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com