
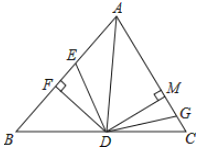
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 于
于![]() ,
,![]() 于
于![]() ,并且
,并且![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 点向
点向![]() 点运动,动点
点运动,动点![]() 以
以![]() 的速度从点
的速度从点![]() 向点
向点![]() 运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为
运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为![]() .
.
(1)求证:在运动过程中,不管![]() 取何值,都有
取何值,都有![]() ;
;
(2)当![]() 取何值时,
取何值时,![]() 与
与![]() 全等;
全等;
(3)若![]() ,当
,当![]() 时
时![]() ,求此时
,求此时![]() 的面积
的面积![]() .
.
【答案】(1)证明见解析;(2)当![]() 时,△DFE与△DMG全等;(3)
时,△DFE与△DMG全等;(3)![]()
【解析】
(1)由角平分线的性质可知DF=DM,所以△AED和△DGC的面积转化为底AE和CG的比值,根据路程=速度×时间求出AE和CG的长度即可证明在运动过程中,不管取何值,都有![]() ;
;
(2)分两种情况进行讨论:①当0<t<3时,②当3<t<5时,分别根据△DFE≌△DMG,得出EF=GM,据此列出关于t的方程,进行求解即可;
(3)利用等高三角形的面积比等于对应底的比,即可求得答案.
(1)∵![]() 是
是![]() 的平分线, DF⊥AB,DM⊥AC,
的平分线, DF⊥AB,DM⊥AC,
∴DF=DM,
∵![]()
∴![]() ,
,
∵点E以3cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴在运动过程中,不管取何值,都有![]() .
.
(2)∵![]() 是
是![]() 的平分线, DF⊥AB,DM⊥AC,
的平分线, DF⊥AB,DM⊥AC,
∴![]() ,
,
∴![]() ,
,
①当0<t<3时,点G在线段CM上,点E在线段AF上. ![]() ,
,
∴![]() ,
,
∴![]() (不合题意,舍去);
(不合题意,舍去);
②当3<t<5时,点G在线段AM上,点E在线段AF上.![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述当![]() 时,△DFE与△DMG全等;
时,△DFE与△DMG全等;
(3)∵![]() ,
,
∴![]() (
(![]() ),
),
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() (
(![]() ),
),
∴![]() (
(![]() ),
),
∵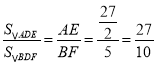 ,
,![]() ,
,
∴![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,秋千链子的长度为4 m,当秋千向两边摆动时,两边的最大摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为( )
A. 2 m B. (4-![]() ) m C. (4-2
) m C. (4-2![]() ) m D. (4-2
) m D. (4-2![]() ) m
) m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边AC上,连接BD,点E在边AB上,△BCD和△BED关于BD对称,若△ADE是等腰三角形,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A. 15° B. 75°或15° C. 105°或15° D. 75°或105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
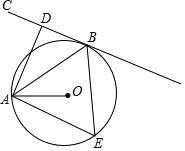
(1)求证:AB平分∠OAD;
(2)若点E是优弧 ![]() 上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com