
【题目】(1)计算: ![]() ﹣2sin45°+(2﹣π)0﹣(
﹣2sin45°+(2﹣π)0﹣(![]() )﹣1;
)﹣1;
(2)先化简,再求值![]() (a2﹣b2),其中a=
(a2﹣b2),其中a=![]() ,b=﹣2
,b=﹣2![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
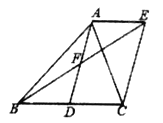
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌ODFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A. B两地果园分别有苹果30吨和40吨,C. D两地的农贸市场分别需求苹果20吨和50吨。已知从A. B两地到C. D两地的运价如表:
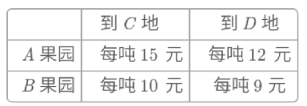
(1)填空:若从A果园运到C地的苹果为10吨,则从A果园运到D地的苹果为___吨,从B果园运到C地的苹果为___吨,从B果园运到D地的苹果为___吨,总运输费为___元;
(2)如果总运输费为750元时,那么从A果园运到C地的苹果为多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个式子:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,
+1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,![]() ),和(5,
),和(5,![]() )都是“共生有理数对”.
)都是“共生有理数对”.
(1)数对(﹣2,1)和(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(a,﹣![]() )是“共生有理数对”,求a的值.
)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
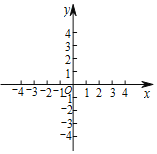
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
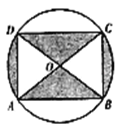
A. 5πcm2 B. 10πcm2 C. 15πcm2 D. 20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个正方形ABCD,点P是边BC上一点.将![]() 绕点A逆时针方向旋转90°得到
绕点A逆时针方向旋转90°得到![]() (点B,P的对应点分别是
(点B,P的对应点分别是![]() )
)
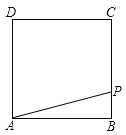
(1)画出旋转后所得到的![]() ;
;
(2)联结![]() ,设
,设![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() 的面积;
的面积;
(3)若![]() 的面积为18,
的面积为18,![]() 的面积为5,试求PC的长.
的面积为5,试求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com