
【题目】下列两个式子:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,
+1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,![]() ),和(5,
),和(5,![]() )都是“共生有理数对”.
)都是“共生有理数对”.
(1)数对(﹣2,1)和(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(a,﹣![]() )是“共生有理数对”,求a的值.
)是“共生有理数对”,求a的值.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
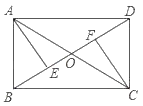
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.
(1)求证:AE=CF.
(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
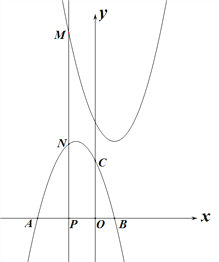
【题目】如图,抛物线T1:y=-x2-2x+3,T2:y=x2-2x+5,其中抛物线T1与x 轴交于A、B两点,与y轴交于C点.P点是x轴上一个动点,过P点并且垂直于x轴的直线与抛物线T1和T2分别相交于N、M两点.设P点的横坐标为t.
(1)用含t的代数式表示线段MN的长;当t为何值时,线段MN有最小值,并求出此最小值;
(2)随着P点运动,P、M、N三点的位置也发生变化.问当t何值时,其中一点是另外两点连接线段的中点?
(3)将抛物线T1平移, A点的对应点为A'(m-3,n),其中![]() ≤m≤
≤m≤![]() ,且平移后的抛物线仍经过C点,求平移后抛物线顶点所能达到的最高点的坐标.
,且平移后的抛物线仍经过C点,求平移后抛物线顶点所能达到的最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调到x元时,销售量为y千克,已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)如果某商品的成本价是20元/千克,为使某一天的利润为780元,那么这一天的销售价应为多少元?(利润=销售总金额﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
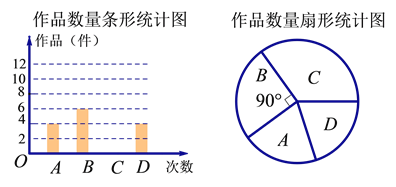
【题目】某中学艺术节期间,学校向学生征集书画作品,学校从全校30个班中随机抽取了4个班 (用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据以上信息,回答下列问题:
(1)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(2)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,![]() ,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
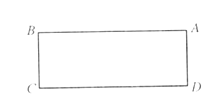
(1)画出长方形EFGD;
(2)连接BD、DF、BF,请用含有a、b的代数式表示![]() 的面积;
的面积;
(3)如果BF交CD于点H,请用含有a、b的代数式表示CH的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com