
【题目】如图,O是直线AB上一点,OD是∠BOC的平分线.

(1)写出图中互补的角;
(2)若∠AOC=53°18′,求∠AOD的度数.
【答案】(1)∠AOC与∠BOC,∠BOD与∠AOD,∠COD与∠AOD;(2)116°39′
【解析】
(1)利用邻补角的定义和角平分线的定义可得互补的角有三对;
(2)先根据平角的定义可得∠BOC的度数,由角平分线可得∠BOD的度数,最后利用邻补角的定义可得结论.
解:(1)∵OD是∠BOC的平分线,
∴∠COD=∠BOD,
∴互补的角有:∠AOC与∠BOC,∠BOD与∠AOD,∠COD与∠AOD.
(2)∵O是直线AB上一点,
∴∠AOB=180°,
∴∠BOC=180°﹣∠AOC=180°﹣53°18′=126°42′,
∵OD是∠BOC的平分线,
∴∠BOD=![]() ∠BOC=
∠BOC=![]() ×126°42′=63°21′.
×126°42′=63°21′.
∴∠AOD=180°﹣∠BOD=180°﹣63°21′=116°39′.


科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句画图:
(1)画∠AOB=120°;
(2)画∠AOB的角平分线OC;
(3)反向延长OC得射线OD;
(4)分别在射线OA、OB、OD上画线段OE=OF=OG=2cm;
(5)连接EF、EG、FG;
(6)你能发现EF、EG、FG有什么关系?∠EFG、∠EGF、∠GEF有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
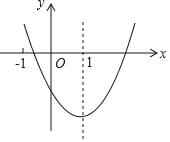
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
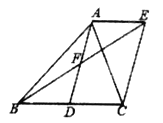
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌ODFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
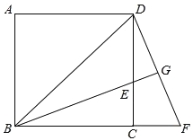
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
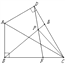
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,BC=2![]() ,△ADC与△ABC关于AC对
,△ADC与△ABC关于AC对
称,点E、F分别是边DC、BC上的任意一点,且DE=CF,BE、DF相交于点P,则CP的最小值为( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个式子:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,
+1.给出定义如下:我们称使等式a﹣b=ab+1成立的一对有理数a,b为“共生有理数对”,记为(a,b),数对(2,![]() ),和(5,
),和(5,![]() )都是“共生有理数对”.
)都是“共生有理数对”.
(1)数对(﹣2,1)和(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(a,﹣![]() )是“共生有理数对”,求a的值.
)是“共生有理数对”,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com