
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
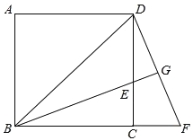
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长
【答案】(1)证明见解析(2) 4
【解析】
试题分析:(1)根据图形的旋转的性质可得△BCE≌△DCF,可得∠FDC=∠EBC,根据BE平分∠DBC,可得∠DBE=∠EBC,从而得到∠FDC=∠EBD,∠DGE是公共角可得出结论;(2)先求出BD=BF,BG⊥DF,求出BE=DF=2DG,根据相似求出DG的长,即可求出答案.
试题解析:(1)∵将△BCE绕点C顺时针旋转到△DCF的位置,∴△BCE≌△DCF,∴∠FDC=∠EBC,∵BE平分∠DBC,∴∠DBE=∠EBC,∴∠FDC=∠EBD,∵∠DGE=∠DGE,∴△BDG∽△DEG;
(2)∵△BCE≌△DCF,∴∠F=∠BEC,∠EBC=∠FDC,∵四边形ABCD是正方形,∴∠DCB=90°,∠DBC=∠BDC=45°,∵BE平分∠DBC,∴∠DBE=∠EBC=22.5°=∠FDC,∴∠BDF=45°+22.5°=67.5°,∠F=90°﹣22.5°=67.5°=∠BDF,∴BD=BF,∵△BCE≌△DCF,∴∠F=∠BEC=67.5°=∠DEG,∴∠DGB=180°﹣22.5°﹣67.5°=90°,即BG⊥DF,∵BD=BF,∴DF=2DG,∵△BDG∽△DEG,BG·EG=4,∴![]() ,∴BG·EG=DG·DG=4,∴DG=2,∴BE=DF=2DG=4.
,∴BG·EG=DG·DG=4,∴DG=2,∴BE=DF=2DG=4.


科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
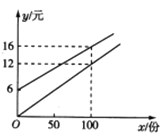
(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
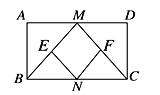
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点,当AB:AD=___________时,四边形MENF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准重量,超过的千克数记为正数,不足的千克数记为负数换后的记录如下:
千克为标准重量,超过的千克数记为正数,不足的千克数记为负数换后的记录如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .回答下列问题上:
.回答下列问题上:
(1)这![]() 筐白菜中最接近标准重量的这筐白菜重 千克.
筐白菜中最接近标准重量的这筐白菜重 千克.
(2)与标准重量比较, ![]() 筐白菜总计超过多少千克或不足多少千克?
筐白菜总计超过多少千克或不足多少千克?
(3)若白菜每千克![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3) 点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似,若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
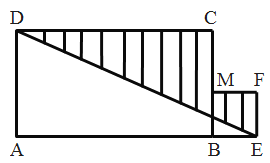
【题目】如图,已知长方形ABCD与正方形BEFM,且A、B、E在一直线上,已知AB=a,BC=b,BE=c,且a>b>c>0.设△ADE的面积为S1.
(1)用含a、b、c的代数式表示S1;
(2)正方形BEFM绕B顺时针旋转180度得到正方形BEFM,连接DM,用含a、b、c的代数式表示△DCM的面积为S2;
(3)请比较S1与S2的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
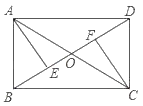
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.
(1)求证:AE=CF.
(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调到x元时,销售量为y千克,已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)如果某商品的成本价是20元/千克,为使某一天的利润为780元,那么这一天的销售价应为多少元?(利润=销售总金额﹣成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com