
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75) 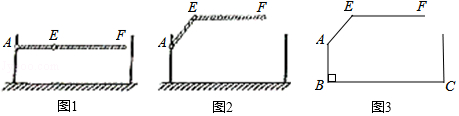
【答案】解:过点E作EG⊥BC于点G,AH⊥EG于点H. 
∵EF∥BC,
∴∠GEF=∠BGE=90°
∵∠AEF=143°,
∴∠AEH=53°.
∴∠EAH=37°.
在△EAH中,AE=1.2,∠AHE=90°,
∴sin∠EAH=sin 37°
∴ ![]()
∴EH=1.2×0.6=0.72.
∵AB⊥BC,
∴四边形ABGH为矩形.
∵GH=AB=1.2,
∴EG=EH+HG=1.2+0.72=1.92≈1.9
【解析】过点E作EG⊥BC于点G,AH⊥EG于点H,则∠AHE=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.


科目:初中数学 来源: 题型:
【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( ) 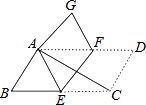
A.135°
B.120°
C.115°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D.求证:(1)∠ECD=∠EDC;(2)OE是CD的垂直平分线.
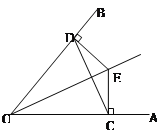
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由,将过程补充完整:
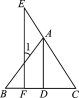
如图,已知AD⊥BC于点D,EF⊥BC于点F,AD平分∠BAC.求证:∠E=∠1.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=∠EFC=90°(垂直的定义).
∴____________(_____________).
∴∠1=_____(_____________),
∠E=_____(_______________).
又∵AD平分∠BAC(已知),
∴_____=________.
∴∠1=∠E(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G. 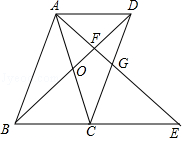
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() =
=![]() =
=![]() +
+![]() =1+
=1+![]() ,
,![]() =
=![]() =
=![]() +
+![]() =2+
=2+![]() ,则
,则![]() 和
和![]() 都是“和谐分式”.
都是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是______(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =______+______;
=______+______;
(3)应用:先化简![]() -
-![]() ÷
÷![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有四条互相不平行的直线l1、l2、l3、l4所截出的七个角,关于这七个角的度数关系,下列结论正确的是( )
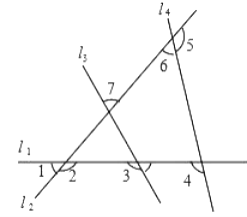
A. ∠2=∠4+∠7 B. ∠3=∠1+∠7
C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
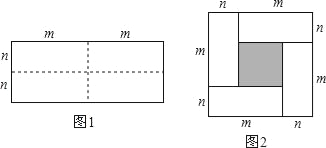
(1)直接写出图2中的阴影部分面积;
(2)观察图2,请直接写出下列三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com