练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在ABCD中，∠ACB=25°，现将ABCD沿EF折叠，使点C与点A重合，点D落在G处，则∠GFE的度数（ ）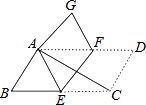
    A.135°
    B.120°
    C.115°
    D.100°

    【答案】C
    【解析】解：由折叠可得：∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE， ∵∠EAC+∠ECA+∠AEC=180°，
    ∴∠AEC=130°，
    ∴∠FEC=65°，
    ∵四边形ABCD是平行四边形，
    ∴AD∥BC，
    ∴∠DFE+∠FEC=180°，
    ∴∠DFE=115°，
    ∴∠GFE=115°，
    故选：C．
    首先根据折叠找到对应相等的角∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE，然后根据三角形内角和可算出∠AEC，进而可得∠FEC的度数，再根据平行四边形的性质可得∠DFE=115°，进而可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读理解：阅读下列材料：已知二次三项式2x2+x+a有一个因式是（x+2），求另一个因式以及a 的值

    解：设另一个因式是（2x+b），

    根据题意，得2x2+x+a=(x+2)(2x+b)，

    展开，得2x2+x+a =2x2+(b+4)x+2b，

    所以，解得，

    所以，另一个因式是（2x3），a 的值是6.

    请你仿照以上做法解答下题：已知二次三项式3x2 10x m 有一个因式是（x+4），求另一个因式以及m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为 的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=4，则OP的长为（ ）
    A.1
    B.
    C.2
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

    国际比赛的足球场长在100m到110m之间，宽在64m到75m之间，为了迎接2015年的亚洲杯，某地建设了一个长方形的足球场，其长是宽的1.5倍，面积是7560m2．请你判断这个足球场能用于国际比赛吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图一，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x﹣2经过A、C两点，且AB=2．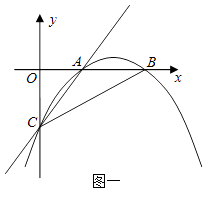

    （1）求抛物线的解析式；
    （2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s= ，当t为何值时，s有最小值，并求出最小值．

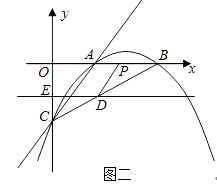
    （3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：已知点A、B是反比例函数y=﹣ 上在第二象限内的分支上的两个点，点C（0，3），且△ABC满足AC=BC，∠ACB=90°，则线段AB的长为 ．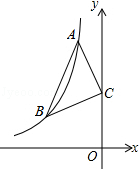

    查看答案和解析>>

    科目：初中数学 来源： 题型：

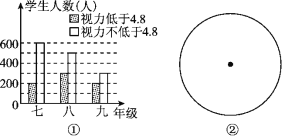
    【题目】某学习小组对所在城区初中学生的视力情况进行抽样调查，图①是调查小组根据调查结果画出的条形统计图．请根据图中信息解决下列问题：

    (1)本次调查活动中共抽查了多少名学生？

    (2)请估算该城区视力不低于4.8的学生所占的比例，用扇形统计图的形式在图②中表示出来．

    (3)假设该城区八年级共有4 000名学生，请估计这些学生中视力低于4.8的学生约有多少名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（ ）

    A. 1︰1︰1

    B. 1︰2︰3

    C. 2︰3︰4

    D. 3︰4︰5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为多少米？（结果精确到0.1．参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）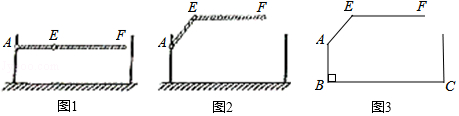

    查看答案和解析>>

    同步练习册答案