
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动一周,且速度为每秒
的路径运动一周,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.
(![]() )出发
)出发![]() 秒后,求
秒后,求![]() 的周长.
的周长.
(![]() )问
)问![]() 为何值时,
为何值时, ![]() 为等腰三角形?
为等腰三角形?
(![]() )另有一点
)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动一周,且速度为每秒
的路径运动一周,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分?
的周长分成相等的两部分?

【答案】(![]() )
)![]() 的周长为
的周长为![]() ;(
;(![]() )当
)当![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 时,
时, ![]() 为等腰三角形;(
为等腰三角形;(![]() )当
)当![]() 为
为![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
【解析】试题分析:(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长;
(2)因为AB与CB,由勾股定理得AC=4 因为AB为5cm,所以必须使AC=CB,或CB=AB,所以必须使AC或AB等于3,有两种情况,△BCP为等腰三角形;
(3)分类讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6.
试题解析:(![]() )
)![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,动点
,动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,
,
∴出发![]() 秒后,
秒后, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的周长为:
的周长为: ![]() .
.
(![]() )①若
)①若![]() 在边
在边![]() 上时,
上时, ![]() ,
,
此时用时![]() ,
, ![]() 为等腰三角形.
为等腰三角形.
②若![]() 在
在![]() 边上时,有三种情况:
边上时,有三种情况:
当![]() ,此时
,此时![]() ,
, ![]() 运动的路程为
运动的路程为![]() ,
,
所以用时为![]() ,
, ![]() 为等腰三角形,
为等腰三角形,
当![]() ,过
,过![]() 作斜边
作斜边![]() 的高,根据面积法求得高为
的高,根据面积法求得高为![]() ,
,
作![]() 于点
于点![]() ,
,
在![]() 中,
中, ![]() ,
,
所以![]() ,
,
所以![]() 运动的路程为
运动的路程为![]() ,
,
则用的时间为![]() ,
, ![]() 为等腰三角形.
为等腰三角形.
③若![]() ,此时
,此时![]() 应该为斜边
应该为斜边![]() 的中点,
的中点, ![]() 运动的路程为
运动的路程为![]() ,
,
则所用的时间为![]() ,
, ![]() 为等腰三角形,
为等腰三角形,
综上所述,当![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 时,
时, ![]() 为等腰三角形;
为等腰三角形;
(![]() )当
)当![]() 点在
点在![]() 上,
上, ![]() 在
在![]() 上,则
上,则![]() ,
, ![]() ,
,
∵直线![]() 把
把![]() 的周长分成相等的两部分,
的周长分成相等的两部分,
∴![]() ,
, ![]() ,
,
当![]() 点在
点在![]() 上,
上, ![]() 在
在![]() 上,则
上,则![]() ,
, ![]() ,
,
∵直线![]() 把
把![]() 的周长分成相等的两部分,
的周长分成相等的两部分,
∴![]() ,
, ![]() ,
,
∴当![]() 为
为![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“367人中有2人同月同日生”为必然事件
B.检测某批次灯泡的使用寿命,适宜用全面调查
C.可能性是1%的事件在一次试验中一定不会发生
D.数据3,5,4,1,﹣2的中位数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
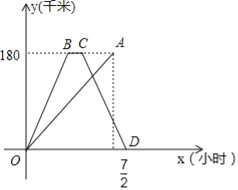
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查显示:手机每平方厘米就驻扎了120000个细菌,按照这样的推算,整部手机起码有上百万个细菌.“手机控”的同学们,你可知道这个可怕的事实哦!请将120000用科学记数法表示为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b=![]() .
.
(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
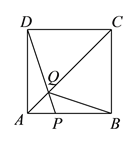
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com