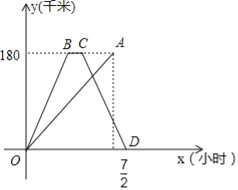
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：

（1）请直接写出快、慢两车的速度；

（2）求快车返回过程中y（千米）与x（小时）的函数关系式；

（3）两车出发后经过多长时间相距90千米的路程？

参考答案：

【答案】（1）慢车的速度60千米/时，快车的速度120千米/时；

（2）y=﹣120x+420（2≤x≤）；（3）或或小时

【解析】试题分析：（1）根据路程与相应的时间，求得慢车的速度，再根据慢车速度是快车速度的一半，求得快车速度；

（2）先求得点C的坐标，再根据点D的坐标，运用待定系数法求得CD的解析式；

（3）分三种情况：在两车相遇之前；在两车相遇之后；在快车返回之后，分别求得时间即可．

试题解析：（1）慢车的速度千米/时，

快车的速度=60×2=120千米/时；

（2）快车停留的时间： （小时），

（小时），即

设CD的解析式为： 则

将代入，得

解得，

∴快车返回过程中y（千米）与x（小时）的函数关系式为

（3）相遇之前：

解得

相遇之后：

解得

快车从甲地到乙地需要小时，

快车返回之后：

解得

综上所述，两车出发后经过或 或小时相距90千米的路程．

关闭