
【题目】四边形ABCD为菱形,BD为对角线,在对角线BD上任取一点E,连接CE,把线段CE绕点C顺时针旋转得到线段CF,使得∠ECF=∠BCD ,点E的对应点为点F,连接DF.
(1)如图1,求证:BE=DF;
(2)如图2,若DF=![]() CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.
CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.


【答案】(10证明见解析;(2)![]() .
.
【解析】试题分析:(1)先根据∠ECF=∠BCD,可求证∠ECB=∠DCF,由旋转可得:EC=FC,由菱形的性质可得:BC=CD,根据SAS可证△BCE≌△DCF,所以BE=DF,(2)根据DF=![]() CF=10,可得DF=10,CF=4,由 ∠DFC=2∠BDC,可得: ∠BEF=2∠BDC,根据三角形的性质性质可得:
CF=10,可得DF=10,CF=4,由 ∠DFC=2∠BDC,可得: ∠BEF=2∠BDC,根据三角形的性质性质可得:
∠BEF=∠BDC+∠ECD,所以∠BDC=∠ECD,所以BE=CE=CF=4,所以BD=14,利用相似三角形的判定可证△BCD∽△CED,根据相似三角形的性质可得: ![]() ,然后计算可得DC.
,然后计算可得DC.
试题解析:(1)因为∠ECF=∠BCD,
所以∠ECF-∠ECD=∠BCD-∠ECD,
所以∠ECB=∠DCF,
由旋转可得: EC=FC,
因为菱形ABCD,
所以BC=CD,
在△BCE和△DCF中,
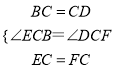 ,
,
所以△BCE≌△DCF,
所以BE=DF,
(2)因为DF=![]() CF=10,所以DF=10,CF=4,
CF=10,所以DF=10,CF=4,
因为∠DFC=2∠BDC,所以 ∠BEF=2∠BDC,
又因为∠BEF=∠BDC+∠ECD,
所以∠BDC=∠ECD,
所以BE=CE=CF=4,所以BD=14,
因为△BCD和△CED是等腰三角形,且∠BDC是公共角
所以△BCD∽△CED,所以![]() ,即
,即![]() ,解得CD=
,解得CD=![]() ,
,
所以菱形的边长为![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
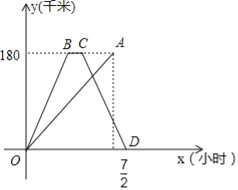
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
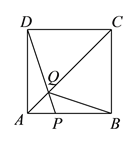
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在⊙O中,弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E,DE交AC于点F.
(1)如图1,求证:BD平分∠ADF;
(2)如图2,连接OC,若OC平分∠ACB,求证:AC=BC;
(3)如图3,在(2)的条件下,连接AB,过点D作DN∥AC交⊙O于点N,若tan∠ADB=![]() ,AB=3
,AB=3![]() ,求DN的长.
,求DN的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,![]() ∥
∥![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
小明的思路是过点![]() 作
作![]() ∥
∥![]() ,通过平行线的性质来求
,通过平行线的性质来求![]() .
.

(1)按照小明的思路,求![]() 的度数;
的度数;
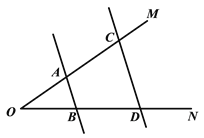
(2)问题迁移:如图,![]() ∥
∥![]() ,点
,点![]() 在射线
在射线![]() 上运动,记
上运动,记![]() ,
,![]() ,当点
,当点![]() 在
在![]() 、
、![]() 两点之间运动时,问
两点之间运动时,问![]() 与
与![]() 、
、![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;

(3)在(2)的条件下,如果点![]() 不在
不在![]() 、
、![]() 两点之间运动时(点
两点之间运动时(点![]() 与点
与点![]() 、
、![]() 、
、![]() 三点不重合),请直接写出
三点不重合),请直接写出![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由

∵∠1=∠2 ( )
∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴_______∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com