Question

【题目】已知：在⊙O中，弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E，DE交AC于点F.

(1)如图1，求证：BD平分∠ADF;

(2)如图2，连接OC，若OC平分∠ACB,求证：AC=BC;

(3)如图3，在（2）的条件下，连接AB,过点D作DN∥AC交⊙O于点N,若tan∠ADB=,AB=3,求DN的长.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）9.

【解析】试题分析:(1)先根据同角的余角相等可证得: ∠ACB＝∠BDE,再根据同弧所对的圆周角相等可得: ∠ACB=∠ADB,所以∠BDE=∠ADB,所以BD平分∠ADF,(2)连接OB,OA,则

△AOC,△BOC是等腰三角形,再证△AOC≌△BOC,根据全等三角形的性质可得:AC=BC,

(3)根据∠ACB=∠ADB, tan∠ADB=,所以tan∠ACB=,所以,可设BH=3x,CH=4x,由勾股定理可得:BC=5x,则AC=5x,所以AH=x,根据勾股定理可得: ,因为AB=,所以可得: ,,解得:x=3,所以DH=4,CH=12,BH=9,BC=15,

所以BD=13,由相似三角形性质可得:BN=,再根据勾股定理解得: DN=9.

试题解析:(1) 因为弦AC⊥弦BD, DE⊥BC于点E,

所以∠ACB+∠DBE＝∠BDE+∠DBE=90°,

所以∠ACB＝∠BDE,

又因为∠ACB=∠ADB,

所以∠BDE=∠ADB,

所以BD平分∠ADF,

(2) 连接OB,OA,则△AOC,△BOC是等腰三角形,

所以∠OCB=∠OBC, ∠OAC=∠OCA,

又因为OC平分∠ACB,

所以∠OCB==∠OCA,

所以∠OBC=∠OAC,

在△AOC和△BOC中,

,

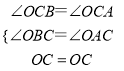所以△AOC≌△BOC,

所以AC=BC,

(3)因为∠ACB=∠ADB, tan∠ADB=,

所以tan∠ACB=,所以,可设BH=3x,CH=4x,由勾股定理得:BC=5x,

则AC=5x,所以AH=x,

因为AB=,根据勾股定理得: ,

所以得: ,,解得:x=3,

所以BC=15,

设等腰△ACB底边AB上的高为h,由勾股定理可得: ,

根据相似三角形性质可得: ,即,解得BN=,

根据勾股定理可得:DN==.