
【题目】解方程:
(1)![]() (直接开平方法)
(直接开平方法)
(2)![]() (因式分解法)
(因式分解法)
(3)![]() (配方法)
(配方法)
(4)![]() (公式法)
(公式法)
【答案】(1) x1=9, x2=1 ; (2) x1=0, x2=-5 ; (3) x1=2+![]() , x2=2-
, x2=2-![]() ; (4) x1=-4 , x2=1.
; (4) x1=-4 , x2=1.
【解析】试题分析:(1)对原方程两边直接开平方转化为两个一元一次方程,这两个一元一次方程的解即为原方程得解;(2)将方程左边因式分解为两个因式的积,然后分别令这两个因式为0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解;(3)先移项,再配方,然后两边开平方求出方程的解;(4)先确定a、b、c的值,然后求出b2-4ac的值,当b2-4ac≥0时代入求根公式.
试题解析:
(1)x-5=±4,x-5=4或x-5=-4,x1=9,x2=1 ;
(2)x(x+5)=0,x1=0,x2=-5 ;
(3)x2-4x=-1,x2-4x+4=-1+4,(x-2)2=3,x-2=±![]() ,x1=2+
,x1=2+![]() ,x2=2-
,x2=2-![]() ;
;
(4)a=1,b=3,c=-4,Δ=32-4×1×(-4) =25>0,x=![]() ,x1=-4,x2=1.
,x1=-4,x2=1.
故答案为(1)x1=9,x2=1 ;(2)x1=0,x2=-5 ;(3)x1=2+![]() ,x2=2-
,x2=2-![]() ;(4)x1=-4,x2=1.
;(4)x1=-4,x2=1.


科目:初中数学 来源: 题型:
【题目】(本题12分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
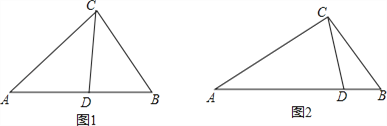
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 坐标.
坐标.
(![]() )在
)在![]() 轴上方存在点
轴上方存在点![]() ,使以点
,使以点![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,画出
全等,画出![]() 并请直接写出点
并请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
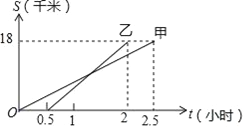
A. 乙比甲先到达B地
B. 乙在行驶过程中没有追上甲
C. 乙比甲早出发半小时
D. 甲的行驶速度比乙的行驶速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中的排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,
① 在甲、乙两人中,总成绩名次靠前的学生是_________;
② 在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
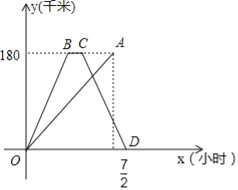
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在⊙O中,弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E,DE交AC于点F.
(1)如图1,求证:BD平分∠ADF;
(2)如图2,连接OC,若OC平分∠ACB,求证:AC=BC;
(3)如图3,在(2)的条件下,连接AB,过点D作DN∥AC交⊙O于点N,若tan∠ADB=![]() ,AB=3
,AB=3![]() ,求DN的长.
,求DN的长.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com