
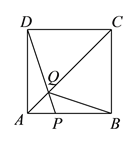
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.
【答案】(1)证明见解析;(2)点![]() 运动时间分别为
运动时间分别为![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)根据SAS证明即可;(2)分别讨论当AD=DQ,AD=AQ,AQ=DQ三种情况.
解:(1)在正方形ABCD中,AB=AD,∠DAC=∠BAC,
在△ADQ和△ABQ中,AD=AB,∠DAC=∠BAC,AQ=AQ,∴△ADQ≌△ABQ.
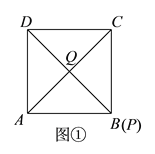
(2)①如图①中,当AQ=DQ时,∠QDA=∠QAD=45°,则点Q为正方形ABCD的中心,点B与点P重合,此时点P运动的时间为t1=4÷1=4(s);
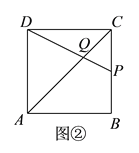
②图②中,当AQ=AD时,则∠ADQ=∠AQD,
∵正方形ABCD边长为4,∴AC![]() ,
,
∴CQ=AC-AQ=![]() ,
,
∵AD∥BC,∴∠CPQ=∠ADQ,
∴∠CPQ=∠AQD=∠CQP,∴CP=CQ=![]() ,
,
∴BP=![]() ,
,
∴P点运动的时间为t2=(4+8-![]() )÷1
)÷1![]() .
.
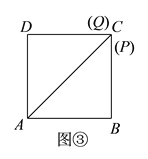
(3)如图③,当AD=DQ时,点C,P,Q三点重合,
此时P点运动时间为t3=(4+4)÷1=8(s).
综上,当△ADQ恰为等腰三角形时,点P运动时间可以为4s, ![]() ,8s.
,8s.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动一周,且速度为每秒
的路径运动一周,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.
(![]() )出发
)出发![]() 秒后,求
秒后,求![]() 的周长.
的周长.
(![]() )问
)问![]() 为何值时,
为何值时, ![]() 为等腰三角形?
为等腰三角形?
(![]() )另有一点
)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动一周,且速度为每秒
的路径运动一周,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分?
的周长分成相等的两部分?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看过西游记的同学都知道:孙悟空会分身术,他摇身一变就变成2个悟空;这两个悟空摇身一变,共变成4个悟空;这4个悟空再变,又变成8个悟空…假设悟空一连变了30次,那么会有_____个孙悟空..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于式子 -(-8)下列理解:①可表示-8的相反数;②可表示-1与-8的积;③可表示-8的绝对值;④运算结果是8.其中理解错误的个数有( )
A.3B.2C.1D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为菱形,BD为对角线,在对角线BD上任取一点E,连接CE,把线段CE绕点C顺时针旋转得到线段CF,使得∠ECF=∠BCD ,点E的对应点为点F,连接DF.
(1)如图1,求证:BE=DF;
(2)如图2,若DF=![]() CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.
CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP,M是直径AB上的动点,A与直线CM上的点连线距离的最小值为d,B与直线CM上的点连线距离的最小值为f.
(1)求证:PC是⊙O的切线;
(2)设OP=![]() AC,求∠CPO的正弦值;
AC,求∠CPO的正弦值;
(3)设AC=9,AB=15,求d+f的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com