
 如图,夏季的一天,身高为1.6m的小玲想测量一下屋前大树BD的高度,她沿着树影BA由树根点B向点A走去,当走到点C时,她的影子顶端正好与树的影子顶端重合,此时测得BC=3.2m,CA=0.8m,由此得出,大树BD=
如图,夏季的一天,身高为1.6m的小玲想测量一下屋前大树BD的高度,她沿着树影BA由树根点B向点A走去,当走到点C时,她的影子顶端正好与树的影子顶端重合,此时测得BC=3.2m,CA=0.8m,由此得出,大树BD=科目:初中数学 来源: 题型:
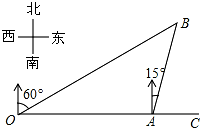 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:| 2 |
| 3 |
| A、366 | B、634 |
| C、650 | D、700 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、不亏不盈 |
| B、亏了7.5元 |
| C、盈了38元 |
| D、盈了15元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com