Question

如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向，测绘员沿主输气道步行1000米到达点C处，测得M小区位于点C的北偏西75°方向，试在主输气管道AC上寻找支管道连接点N，使其到该小区铺设的管道最短，此时AN的长约是（参考：

2

≈1.414，

3

≈1.732）（　　）

• A、366
• B、634
• C、650
• D、700

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：首先过点M作MN⊥AC于点N，由题意可求得∠MAN=30°，∠MCN=45°，然后设MN=x，由三角函数的性质，可表示出AN与CN，继而可得方程：

3

x+x=1000，解此方程即可求得答案．

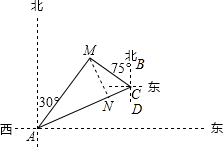解答：解：如图：过点M作MN⊥AC于点N，
根据题意得：∠MAN=60°-30°=30°，∠BCM=75°，∠DCA=60°，
∴∠MCN=180°-75°-60°=45°，
设MN=x米，
在Rt△AMN中，AN=

MN

tan30°

=

3

x（米），
在Rt△CMN中，CN=

MN

tan45°

=x（米），
∵AC=1000米，
∴

3

x+x=1000，
解得：x=500（

3

-1），
∴AN=

3

x≈634．
故选B．

点评：此题考查了方向角问题．此题难度适中，注意构造直角三角形，并能借助于解直角三角形的知识求解是关键，注意数形结合思想与方程思想的应用．