Question

【题目】综合题解方程组和不等式
（1）解方程组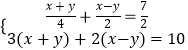
（2）解不等式组 ，并在数轴上画出它的解集．

Answer 1

【答案】
（1）解：原方程组整理可得： ，

①+②，得：8x=24，

解得：x=3，

将x=3代入②，得：15+y=10，

解得：y=﹣5，

则原方程组的解为

（2）解：解不等式4x﹣3＜3（2x+1），得：x＞﹣3，

解不等式 x﹣1＞5﹣ x，得：x＞3，

∴不等式组的解集为x＞3，

将解集表示在数轴上如下：

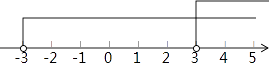
【解析】（1）去分母后y的系数互为相反数，可采用加减消元法;（2）移项、合并同类项，将不等式华为最简形式，按照法则“大大取大”即可解出.
【考点精析】利用解二元一次方程组和不等式的解集在数轴上的表示对题目进行判断即可得到答案，需要熟知二元一次方程组：①代入消元法；②加减消元法；不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈．