
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF. 
(1)求证:△ADF≌△CEF;
(2)试判断△DFE的形状,并说明理由.
【答案】
(1)证明:∵F是AB中点,AC=BC,∠ACB=90°,
∴AF=BF=CF,∠A=∠FCE=45°,
在△ADF和△CEF中,
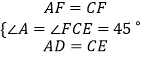 ,
,
∴△ADF≌△CEF(SAS)
(2)解:△DEF是等腰直角三角形.理由如下:
∵△ADF≌△CEF,
∴DF=EF,∠AFD=∠CFE,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFE=90°,即∠DFE=90°,
∴△DEF是等腰直角三角形
【解析】(1)根据F是AB中点,可得AF=BF=CF,∠A=∠FCE=45°,即可证明△ADF≌△CEF;(2)根据△ADF≌△CEF可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可解题.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,![]() ,
,![]() .若S=3,则
.若S=3,则![]() 的值为( )
的值为( )
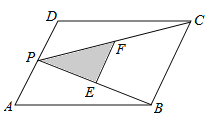
A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( ) 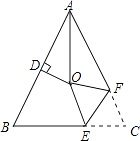
A.72°
B.100°
C.108°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当![]() = 时,四边形ADFE是平行四边形.
= 时,四边形ADFE是平行四边形.
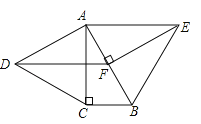
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.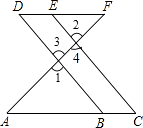
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2()
∠1=∠3()
∴∠2=∠3()
∴∥()
∴∠C=∠ABD ()
又∵∠C=∠D()
∴∠D=∠ABD()
∴AC∥DF()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com