
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
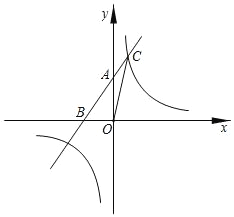
【答案】(1)y=![]() ;(2)1;(3)x<﹣3或0<x<1.
;(2)1;(3)x<﹣3或0<x<1.
【解析】
(1)将点C坐标分别代入直线y=x+2和反比例函数y=![]() ,可求点C坐标,即可求反比例函数的解析式;
,可求点C坐标,即可求反比例函数的解析式;
(2)由题意可得点A(0,2),点B(-2,0),即可求△AOC的面积;
(3)列出方程组可求直线y=x+2和反比例函数y=![]() 的交点坐标,根据图象可求不等式x+2-
的交点坐标,根据图象可求不等式x+2-![]() <0的解集.
<0的解集.
解:(1)∵点C(1,a)在直线y=x+2上,
∴a=1+2=3
∴点C(1,3)
∵点C在反比例函数y=![]() 图象上,
图象上,
∴k=1×3=3
∴反比例函数的解析式y=![]()
(2)∵直线y=x+2与坐标轴相交于A,B两点,
∴点A(0,2),点B(﹣2,0)
∴OA=2
∴S△AOC=![]() ×1×2=1
×1×2=1
(3)∵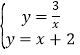
解得:![]() ,
,![]()
∴直线y=x+2与反比例函数y=![]() 的交点为(1,3),(﹣3,﹣1)
的交点为(1,3),(﹣3,﹣1)
∴不等式x+2﹣![]() <0的解集为:x<﹣3或0<x<1.
<0的解集为:x<﹣3或0<x<1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长16m,宽12m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
(1)你认为小强的结果对吗?请说明理由.

(2)请你帮助小颖求出图中的x.
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
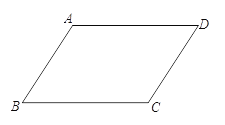
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】物理兴趣小组![]() 位同学在实验操作中的得分情况如下表:
位同学在实验操作中的得分情况如下表:
得分(分) |
|
|
|
|
人数(人) |
|
|
|
|
问:(1)这![]() 位同学实验操作得分的众数是 ,中位数是
位同学实验操作得分的众数是 ,中位数是
(2)这![]() 位同学实验操作得分的平均分是多少?
位同学实验操作得分的平均分是多少?
(3)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
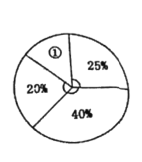
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
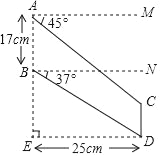
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
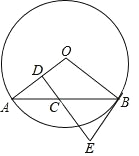
【题目】如图,AB 是⊙O 的一条弦,C 是 AB 的中点,过点 C 作直线垂直于OA 于点 D,交过点 B 的⊙O 的切线于点 E.
(1)求证:BE=CE;
(2)若⊙O 的半径长为 8,AB=12,求 BE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com