
【题目】边长为整数的直角三角形,若其两直角边边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定直角三角形三边之长。
【答案】解:设直角边为a,b(a<b),则a+b=k+2,ab=4k,因为方程的根为整数,故△=(k+2)2-16k为完全平方数。
设(k+2)2-16k=n2 ∴k2-12k+4=n2 ∴(k-6)2-n2=32
∴(k+n-6)(k-n-6)=1×32=2×16=4×8
∵k+n-6>k-n-6 ∴ ![]()
解得 ![]() ,k2=15,k3=12
,k2=15,k3=12
当k2=15时,a+b=17,ab=60 ∴a=15 , b=12 , c=13;当k=12时,a+b=14,ab=48
∴a=6 , b=8 ,c=10
【解析】根据方程的根为整数,得到根的判别式为平方数,然后进行讨论求出k值,得到三角形三边的长.根据直角三角形的直角边是整数,得到方程的根是整数,所以判别式是平方数,讨论求出k的值.然后求出直角三角形三边的长.
【考点精析】利用公式法和求根公式对题目进行判断即可得到答案,需要熟知要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是平行四边形,点
是平行四边形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的动点,若
上的动点,若![]() 是等腰三角形,则点
是等腰三角形,则点![]() 的坐标为_____.
的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,对角线
在第一象限内,对角线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() .将菱形
.将菱形![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位.当点
个单位.当点![]() 落在
落在![]() 的内部时(不包括三角形的边),则
的内部时(不包括三角形的边),则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
查看答案和解析>>
科目:初中数学 来源: 题型:
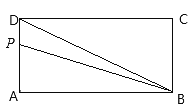
【题目】如图,长方形ABCD中,AB=2cm,BC=4cm,点P按照顺时针方向由点A运动到点D,设点P运动的路程为![]() 图中点P、B、D围成的图形的面积为
图中点P、B、D围成的图形的面积为![]()
(1)写出点P、B、D围成的图形的面积![]() 与
与![]() 之间的关系式和自变量
之间的关系式和自变量![]() 的取值范围;
的取值范围;
(2)当![]() 取何值时,点P、B、D围成的图形的面积等于
取何值时,点P、B、D围成的图形的面积等于![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com