
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
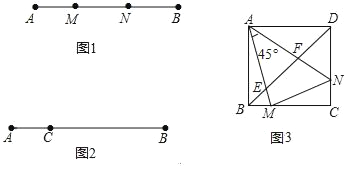
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
【答案】(1)BN=![]() 或5;(2)图形见解析;(3)①证明见解析,②证明见解析.
或5;(2)图形见解析;(3)①证明见解析,②证明见解析.
【解析】试题分析:(1)①当MN为最大线段时,由勾股定理求出BN;由BN为最大线段时,由勾股定理求出BN即可;
(2)①在AB上截取CE=CA,②作AE的垂直平分线,并截取CF=CA,③连接BF,并作BF的垂直平分线,交AB于D;
(3)①如图3,将△ADF绕点A顺时针旋转90°得到△ABH,连接HE,只要证明△EAH≌△EAF,推出EF=HE,再证明∠HBE=90°即可;
②如图,连接FM,EN,证明△AEN和△AFM是等腰直角三角形,推出AM、AN,根据三角形的面积和锐角三角函数求解即可.
试题解析:(1)解:(1)①当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM=![]() =
=![]() =
=![]() ,
,
②当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN=![]() =
=![]() =5,
=5,
综上,BN=![]() 或5;
或5;
(2)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示.
(3)①如图3中,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.
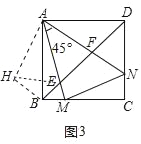
∵∠DAF+∠BAE=90°﹣∠EAF=45°,∠DAF=∠BAH,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AF,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,
∴E、F是线段BD的勾股分割点.
②证明:如图4中,连接FM,EN.
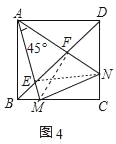
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,∵∠AFE=∠FDN,
∴△AFE∽△DFN,
∴∠AEF=∠DNF,![]() =
=![]() ,
,
∴![]() =
=![]() ,∵∠AFD=∠EFN,
,∵∠AFD=∠EFN,
∴△AFD∽△EFN,
∴∠DAF=∠FEN,
∵∠DAF+∠DNF=90°,
∴∠AEF+∠FEN=90°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM=![]() AF,AN=
AF,AN=![]() AE,
AE,
∵S△AMN=![]() AMANsin45°,
AMANsin45°,
S△AEF=![]() AEAFsin45°,
AEAFsin45°,
∴![]() =
=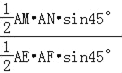 =2,
=2,
∴S△AMN=2S△AEF.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).
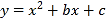
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
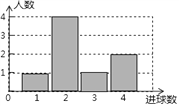
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为检测我市正在销售的酸奶质量,应该采用普查的方式
B. 若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定
C. 抛掷一个正方体骰子,朝上的面的点数为奇数的概率是![]()
D. “打开电视,正在播放广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | |
B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]()
(1)如图①,![]() 与
与![]() 的数量关系为______
的数量关系为______
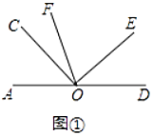
(2)如图①,如果![]() ,请你求出
,请你求出![]() 的度数并说明理由;
的度数并说明理由;
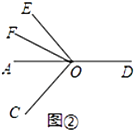
(3)若将图①中的![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的度数
的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
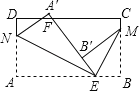
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN,若∠DNA'的度数为α,请用含α的式子表示∠BME的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com