
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】根据题意和函数的图像,可知抛物线的对称轴为直线x=-![]() =2,即b=-4a,变形为4a+b=0,所以(1)正确;
=2,即b=-4a,变形为4a+b=0,所以(1)正确;
由x=-3时,y>0,可得9a+3b+c>0,可得9a+c>-3c,故(2)正确;
因为抛物线与x轴的一个交点为(-1,0)可知a-b+c=0,而由对称轴知b=-4a,可得a+4a+c=0,即c=-5a.代入可得7a﹣3b+2c=7a+12a-5a=14a,由函数的图像开口向下,可知a<0,因此7a﹣3b+2c<0,故(3)不正确;
根据图像可知当x<2时,y随x增大而增大,当x>2时,y随x增大而减小,可知若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1=y3<y2,故(4)不正确;
,y2)、点C(7,y3)在该函数图象上,则y1=y3<y2,故(4)不正确;
根据函数的对称性可知函数与x轴的另一交点坐标为(5,0),所以若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<x2,故(5)正确.
正确的共有3个.
故选:B.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】希腊数学家丢番图(公元3-4世纪)的墓碑上记载着: “他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲痛中度过了四年,也与世长辞了.”
根据以上信息,请你算出:
(1)丢番图的寿命;
(2)丢番图开始当爸爸时的年龄;
(3)儿子死时丢番图的年龄.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(3,7)和B(﹣8,-4).
(1)求直线的解析式;
(2)求出该直线与x轴、y轴的交点坐标。并求出直线与两坐标轴围成三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
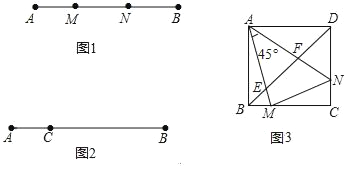
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9、11……按一定规律排成如下表:

图中的![]() 字框框住了四个数,若将
字框框住了四个数,若将![]() 字框上下左右移动,按同样的方式可框住另外的四个数.
字框上下左右移动,按同样的方式可框住另外的四个数.
(1)数表中从小到大排列的第9个数是17,第40个数是______,第100个数是______,第![]() 个数是______;
个数是______;
(2)设![]() 字框内处于中间且靠上方的数是整个数表中从小到大排列的第
字框内处于中间且靠上方的数是整个数表中从小到大排列的第![]() 个数,请你用含
个数,请你用含![]() 的代数式表示
的代数式表示![]() 字框中的四个数的和;
字框中的四个数的和;
(3)若将![]() 字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由.
字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
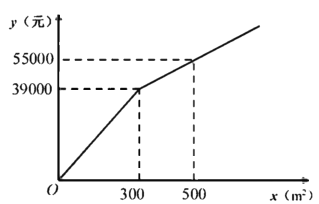
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com