
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]()
(1)如图①,![]() 与
与![]() 的数量关系为______
的数量关系为______
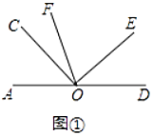
(2)如图①,如果![]() ,请你求出
,请你求出![]() 的度数并说明理由;
的度数并说明理由;
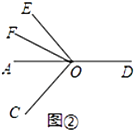
(3)若将图①中的![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的度数
的度数
科目:初中数学 来源: 题型:
【题目】如图所示,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.
 ……
……
(1)第2个图形中,火柴棒的根数是________.
(2)第3个图形中,火柴棒的根数是________.
(3)第n个图形中,火柴棒的根数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
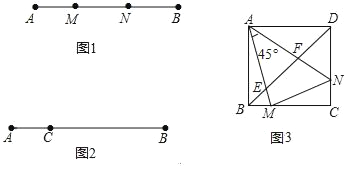
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
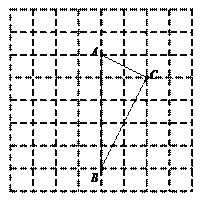
【题目】如图,在由边长为1的小正方形组成的网格图中,有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形.)
(1)△ABC是 三角形(填“锐角”、“直角”或“钝角”);
(2)若P、Q分别为线段AB、BC上的动点,当PC+PQ取得最小值时,
① 在网格中用无刻度的直尺,画出线段PC、PQ.(请保留作图痕迹.)
② 直接写出PC+PQ的最小值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线BD上一点,并且AD=DE,过点E作EF⊥BD交AB于点F.
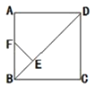
(1)求证:AF=BE,(2)若正方形的边长为1,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:
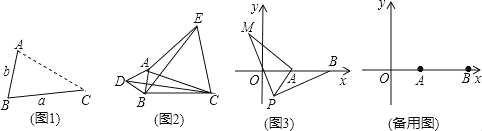
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com