【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球，它们除颜色外完全相同．每次从袋中摸出1个球，记下颜色后放回搅匀再摸．摸球实验中，统计得到下表中的数据：
摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
由此可以估计摸到黄球的概率约为________（精确到0.1）．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图所示，已知□ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．
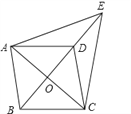
（1）四边形ABCD是菱形吗？请说明理由；
（2）若∠AED=2∠EAD，试说明四边形ABCD是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在五张正面分别写有数字﹣2，﹣1，0，1，2的卡片，它们的背面完全相同，现将这五张卡片背面朝上洗匀．
（1）从中任意抽取一张卡片，则所抽卡片上数字的绝对值不大于1的概率是 ；
（2）先从中任意抽取一张卡片，以其正面数字作为a的值，然后再从剩余的卡片随机抽一张，以其正面的数字作为b的值，请用列表法或画树状图法，求点Q（a，b）在第二象限的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：∠MON＝80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D．设∠OAC＝α．
（1）如图1，若AB∥ON，则：
①∠ABO的度数是 ；
②如图2，当∠BAD＝∠ABD时，试求α的值（要说明理由）；
（2）如图3，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，直接写出α的值；若不存在，说明理由．（自己画图）
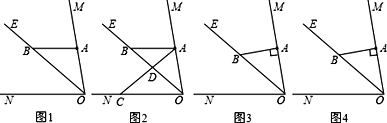
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】著名的瑞士数学家欧拉曾指出：可以表示为四个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为四个整数平方之和，即
，这就是著名的欧拉恒等式，有人称这样的数为“不变心的数”．实际上，上述结论可减弱为：可以表示为两个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为两个整数平方之和．
【动手一试】
试将
改成两个整数平方之和的形式． 
；
【阅读思考】
在数学思想中，有种解题技巧称之为“无中生有”．例如问题：将代数式
改成两个平方之差的形式．解：原式
﹒
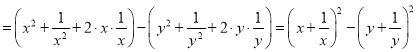【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题：将代数式
改成两个整数平方之和的形式（其中a、b、c、d均为整数），并给出详细的推导过程﹒
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（ ）
A. OE=
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
