
����Ŀ����������ʿ��ѧ��ŷ����ָ�������Ա�ʾΪ�ĸ�����ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ�ĸ�����ƽ��֮�ͣ���![]()
![]() �������������ŷ�����ʽ�����˳���������Ϊ�������ĵ�������ʵ���ϣ��������ۿɼ���Ϊ�����Ա�ʾΪ��������ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ��������ƽ��֮�ͣ�
�������������ŷ�����ʽ�����˳���������Ϊ�������ĵ�������ʵ���ϣ��������ۿɼ���Ϊ�����Ա�ʾΪ��������ƽ��֮�͵ļס���������ˣ���˻���Ȼ���Ա�ʾΪ��������ƽ��֮�ͣ�
������һ�ԡ�
�Խ�![]() �ij���������ƽ��֮�͵���ʽ��
�ij���������ƽ��֮�͵���ʽ�� ![]() ��
��
���Ķ�˼����
����ѧ˼���У����ֽ��⼼�ɳ�֮Ϊ���������������������⣺������ʽ![]() �ij�����ƽ��֮�����ʽ���⣺ԭʽ
�ij�����ƽ��֮�����ʽ���⣺ԭʽ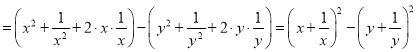 �q
�q
��������⡿
�������������������˼��������������ĵ��������⣺������ʽ![]() �ij���������ƽ��֮�͵���ʽ������a��b��c��d��Ϊ����������������ϸ���Ƶ����̩q
�ij���������ƽ��֮�͵���ʽ������a��b��c��d��Ϊ����������������ϸ���Ƶ����̩q
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲죺����2��1=��2������2��2=4������2��3=��8������2��4=16������2��5=��32������2��6=64������2��7=��128���÷��ֵĹ���д������2��2017��ĩλ������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ���װ�к졢�ס���3����ɫ�����ɸ�С�����dz���ɫ����ȫ��ͬ��ÿ�δӴ�������1��������ɫ��Żؽ�������������ʵ���У�ͳ�Ƶõ��±��е����ݣ�
������� | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
���ֺ����Ƶ�� | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
���ְ����Ƶ�� | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
�ɴ˿��Թ�����������ĸ���ԼΪ________����ȷ��0.1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���һԪ���η���ax2+bx+c=0��a��0������a+b+c=0����ô���dz��������Ϊ�����������̣����һԪ���η���ax2+bx+c=0��a��0������a��b+c=0��ô���dz��������Ϊ�����������̣����һ��һԪ���η��̼����������������������������������dz�֮Ϊ�����������������������������������н�����ȷ���ǣ� ��
A. ��������֮�͵���0
B. ������һ������0
C. ������������ȵ�ʵ����
D. ��������֮������0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ�Լס������˵������ѧ����ɼ�����ͳ�ƣ��ó�������β���ɼ���ƽ���־�Ϊ90�֣�����ֱ���S2��=51��S2��=12���ɴ˿�֪��������
A. �ױ��ҵijɼ��ȶ�B. �ұȼijɼ��ȶ�
C. �ס������˵ijɼ�һ���ȶ�D. ��ȷ��˭�ijɼ����ȶ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com