
【题目】已知二次函数y=2x2﹣mx﹣m2
(1)求证:对于任意实数m,二次函数y=2x2﹣mx﹣m2的图象与x轴总有公共点;
(2)若这个二次函数图象与x轴有两个公共点A,B,且B点坐标为(1,0),求A点坐标.
【答案】
(1)证明:2x2﹣mx﹣m2=0,
△=(﹣m)2﹣4×2×(﹣m2)
=m2+8m2
=9m2≥0,
∴对于任意实数m,二次函数y=2x2﹣mx﹣m2的图象与x轴总有公共点
(2)解:由题意得,2×12﹣m﹣m2=0,
整理得,m2+m﹣2=0,
解得,m1=1,m2=﹣2,
当m=1时,二次函数为y=2x2﹣x﹣1,
当y=0时,2x2﹣x﹣1=0,
解得,x1=1,x2=﹣ ![]() ,
,
则点A的坐标为(﹣ ![]() ,0),
,0),
当m=﹣2时,二次函数为y=2x2+2x﹣4,
当y=0时,2x2﹣x﹣1=0,
解得,x1=1,x2=﹣2,
则点A的坐标为(﹣2,0),
终上所述,A点坐标为(﹣ ![]() ,0)或(﹣2,0)
,0)或(﹣2,0)
【解析】(1)利用一元二次方程根的判别式证明;(2)根据题意求出m的值,解一元二次方程即可.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若 ![]() ,则x+y的取值范围是( )
,则x+y的取值范围是( ) 
A.[﹣4,4]
B.![]()
C.[﹣5,5]
D.[﹣6,6]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,cosA= ![]() ,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( ) 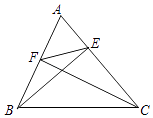
A.1:2
B.1:3
C.1:4
D.1:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD= ![]() .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农业现代化是我国“十三五”的重要规划之一,某地农民积极响应政府号召,自发成立现代新型农业合作社,适度扩大玉米种业规模,今年,合作社600亩玉米喜获丰收.合作社打算雇佣玉米收割机收割玉米,现有A,B两种型号收割机可供选择,且每台B种型号收割机每天的收个亩数是A种型号的1.5倍,如果单独使用一台收割机将600亩玉米全部收割完,A种型号收割机比B种型号收割机多用10天. 
(1)求A,B两种型号收割机每台每天收个玉米的亩数;
(2)已知A种型号收割机收费是45元/亩,B种型号收割机收费是50元/亩,经过研究,合作社计划同时雇佣A,B两种型号收割机各一台合作完成600亩玉米的收割任务,则合作社需要支付的玉米收割总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com