
【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD= ![]() .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
【答案】
(1)
解:∵四边形ABCD是菱形,
∴BA=BC,∠ABE=∠CBE.
在△ABE和△CBE中, 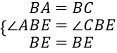
又∵BE=BE,
∴△ABE≌△CBE
∴AE=CE.
(2)
解:连接AC,交BD于点O,过点A作AH⊥BC,过点E作EF⊥BC,如图1所示:
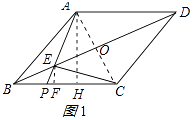
垂足分别为点H、F.
∵四边形ABCD是菱形,
∴AC⊥BD.
∵AB=5, ![]() ,
,
∴AO=OC= ![]() ,BO=OD=
,BO=OD= ![]() .
.
∵ ![]() ,
,
∴AH=4,BH=3.
∵AD∥BC,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵EF∥AH,
∴ ![]() ,
,
∴ ![]() .
.
∴ ![]()
(3)
解:因为点P在线段BC的延长线上,所以∠EPC不可能为直角.如图2所示:
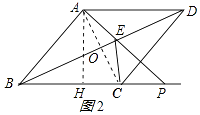
①当∠ECP=90°时
∵△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∵ ![]() ,
,
∴ ![]() ,∴BP=
,∴BP= ![]() .
.
②当∠CEP=90°时,
∵△ABE≌△CBE,
∴∠AEB=∠CEB=45°,
∴ ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵AD∥BP,
∴ ![]() ,
,
∴ ![]() ,
,
∴BP=15.
综上所述,当△EPC是直角三角形时,线段BP的长为 ![]() 或15
或15
【解析】(1)由菱形的性质得出BA=BC,∠ABD=∠CBD.由SAS证明△ABE≌△CBE,即可得出结论.(2)联结AC,交BD于点O,过点A作AH⊥BC于H,过点E作EF⊥BC于F,由菱形的性质得出AC⊥BD.由三角函数求出AO=OC= ![]() ,BO=OD=
,BO=OD= ![]() .由菱形面积得出AH=4,BH=3.由相似三角形的性质得出
.由菱形面积得出AH=4,BH=3.由相似三角形的性质得出 ![]() ,求出EF的长,即可得出答案;∴
,求出EF的长,即可得出答案;∴ ![]() ,(3)因为点P在线段BC的延长线上,所以∠EPC不可能为直角.分情况讨论:①当∠ECP=90°时,②当∠CEP=90°时,由全等三角形的性质和相似三角形的性质即可得出答案.
,(3)因为点P在线段BC的延长线上,所以∠EPC不可能为直角.分情况讨论:①当∠ECP=90°时,②当∠CEP=90°时,由全等三角形的性质和相似三角形的性质即可得出答案.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣mx﹣m2
(1)求证:对于任意实数m,二次函数y=2x2﹣mx﹣m2的图象与x轴总有公共点;
(2)若这个二次函数图象与x轴有两个公共点A,B,且B点坐标为(1,0),求A点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3. 
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: ![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73.)
≈1.73.)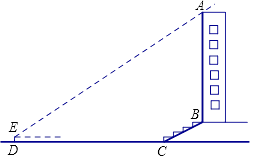
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x﹣c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE 
(1)求证:DEAB=ACBE;
(2)如果AC2=ADAB,求证:AE=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com