
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3. 
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且 ![]() ,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1.
,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1. 
(Ⅰ)证明:直线MD∥平面ABC;
(Ⅱ)求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 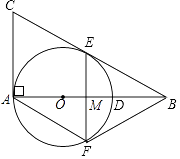
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD= ![]() .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.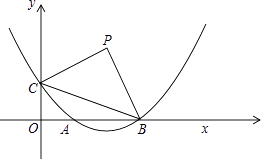
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C. 
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com