
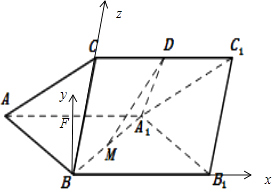
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且 ![]() ,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1.
,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1. 
(Ⅰ)证明:直线MD∥平面ABC;
(Ⅱ)求二面角B﹣AC﹣A1的余弦值.
【答案】解:∵A1D⊥CC1 , 且D为中点,AA1=A1D=2,∴ ![]() , 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
, 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
又 BA∩BA1=B,∴CB⊥平面ABB1A1 ,
取AA1中点F,则BF⊥AA1 , 即BC,BF,BB1两两互相垂直,
以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系如图所示,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), 
(I) 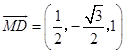 ,设平面ABC的法向量为
,设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 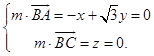 ,取
,取 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
又MD平面ABC,∴直线MD∥平面ABC.
(II) 设平面ACA1的法向量为n=(x1 , y1 , z1), ![]() ,
,
则 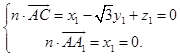 ,取
,取 ![]() ,
,
又由(Ⅰ)知平面ABC的法向量为 ![]() ,
,
设二面角B﹣AC﹣A1为θ,
∴ 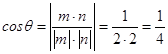 ,
,
∴二面角B﹣AC﹣A1的余弦值为 ![]()
【解析】由已知可得 ![]() ,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1),
,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), ![]() ,利用空间向量求解.
,利用空间向量求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=![]() AB,连接EF,判断四边形ADEF的形状,并加以证明.
AB,连接EF,判断四边形ADEF的形状,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() , 连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
, 连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+m与抛物线x2=4y相切,且与x轴的交点为M,点N(﹣1,0).若动点P与两定点M,N所构成三角形的周长为6.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ) 设斜率为 ![]() 的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN.
的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 ![]() ,则f(x)在[0,k]的最大值h(k)=( )
,则f(x)在[0,k]的最大值h(k)=( )
A.2ln2﹣2﹣(ln2)3
B.﹣1
C.2ln2﹣2﹣(ln2)2k
D.(k﹣1)ek﹣k3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3. 
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 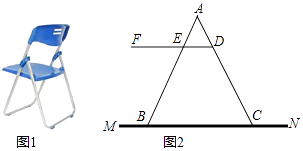
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com