
【题目】函数 ![]() ,则f(x)在[0,k]的最大值h(k)=( )
,则f(x)在[0,k]的最大值h(k)=( )
A.2ln2﹣2﹣(ln2)3
B.﹣1
C.2ln2﹣2﹣(ln2)2k
D.(k﹣1)ek﹣k3
【答案】D
【解析】解:f′(x)=xex﹣2kx=x(ex﹣2k), 令f′(x)=0得x=0或x=ln2k,
令g(k)=k﹣ln2k,则g′(k)=1﹣ ![]() <0
<0
∴g(k)在( ![]() ,1]上是减函数,∴g(k)≥g(1)=1﹣ln2>0,
,1]上是减函数,∴g(k)≥g(1)=1﹣ln2>0,
∴k>ln2k,
∴f(x)在[0,ln2k]上单调递减,在(ln2k,k]上单调递增,
∴f(x)的最大值为f(0)或f(k).
f(k)﹣f(0)=(k﹣1)ek﹣k3+1=(k﹣1)(ek﹣k2﹣k﹣1),
令h(x)=ek﹣k2﹣k﹣1,则h′(k)=ek﹣2k﹣1,h′′(k)=ek﹣2,
令h″(k)=0得k=ln2,
∴h′(k)在( ![]() ,ln2)上单调递减,在(ln2,1]上单调递增,
,ln2)上单调递减,在(ln2,1]上单调递增,
∵h′( ![]() )=
)= ![]() ﹣2<0,h′(1)=e﹣3<0,
﹣2<0,h′(1)=e﹣3<0,
∴h′(k)<0在( ![]() ,1]上恒成立,
,1]上恒成立,
∴h(k)在( ![]() ,1]上是减函数,∴h(k)<h(
,1]上是减函数,∴h(k)<h( ![]() )=
)= ![]() ﹣
﹣ ![]() <0,
<0,
∴f(k)≥f(0),
∴f(x)的最大值为f(k)=(k﹣1)ek﹣k3 ,
故选D.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为 .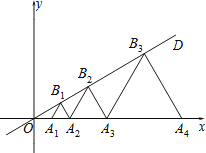
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE,设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为y=ax2+bx+c.
(1)求点D的坐标(用含m的式子表示);
(2)若点G的坐标为(0,﹣3),求该抛物线的解析式;
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=![]() EA?若存在,直接写出点P的坐标;若不存在,说明理由.
EA?若存在,直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为 ![]() ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且 ![]() ,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1.
,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1. 
(Ⅰ)证明:直线MD∥平面ABC;
(Ⅱ)求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 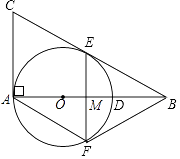
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC= ![]() .
.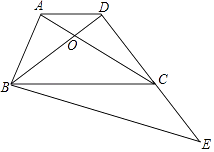
(1)求证:BC2=CDBE;
(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;
(3)如果△DBC∽△DEB,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com