
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE,设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为y=ax2+bx+c.
(1)求点D的坐标(用含m的式子表示);
(2)若点G的坐标为(0,﹣3),求该抛物线的解析式;
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=![]() EA?若存在,直接写出点P的坐标;若不存在,说明理由.
EA?若存在,直接写出点P的坐标;若不存在,说明理由.
【答案】
(1)
解:根据折叠的性质得:CF=AB=m,DF=DB,∠DFC=∠DBA=90°,CE=AE,∠CED=∠AED,
设CD=x,则DF=DB=2m﹣x,
根据勾股定理得:CF2+DF2=CD2,
即m2+(2m﹣x)2=x2,
解得:x=![]() m,
m,
∴点D的坐标为:(![]() m,m);
m,m);
(2)
解:∵四边形OABC是矩形,
∴OA=2m,OA∥BC,
∴∠CDE=∠AED,
∴∠CDE=∠CED,
∴CE=CD=![]() m,
m,
∴AE=CE=![]() m,
m,
∴OE=OA﹣AE=![]() m,
m,
∵OA∥BC,
∴△OEG∽△CDG,
∴![]() ,
,
即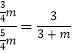 ,
,
解得:m=2,
∴C(0,2),D(![]() ,2),
,2),
作FH⊥CD于H,如图1所示:
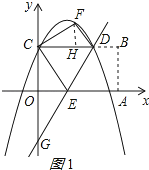
则∠FHC=90°=∠DFC,
∵∠FCH=∠FCD,
∴△FCH∽△DCF,
∴![]() =
=![]() =
=![]() ,
,
即![]()
![]()
![]() ,
,
∴FH=![]() ,CH=
,CH=![]() ,
,![]() +2=
+2=![]() ,
,
∴F(![]() ,
,![]() ),
),
把点C(0,2),D(![]() ,2),F(
,2),F(![]() ,
,![]() )代入y=ax2+bx+c得:
)代入y=ax2+bx+c得:
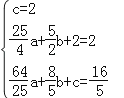 ,
,
解得:a=![]() ,b=
,b=![]() ,c=2,
,c=2,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x+2;
x+2;
(3)
解:存在;点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() );理由如下:
);理由如下:
如图2所示:
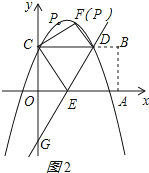
∵CD=CE,CE=EA,
∴CD=EA,
∵线段CD的中点为M,∠DFC=90°,
∴MF=![]() CD=
CD=![]() EA,点P与点F重合,
EA,点P与点F重合,
∴点P的坐标为:(![]() ,
,![]() );
);
由抛物线的对称性得另一点P的坐标为(![]() ,
,![]() );
);
∴在线段CD上方的抛物线上存在点P,使PM=![]() EA,点P的坐标为:(
EA,点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).
【解析】(1)由折叠的性质得出CF=AB=m,DF=DB,∠DFC=∠DBA=90°,CE=AE,设CD=x,则DF=DB=2m﹣x,由勾股定理得出方程,解方程即可得出结果;
(2)证明△OEG∽△CDG,得出比例式,求出m的值,得出C、D的坐标,作FH⊥CD于H,证明△FCH∽△DCF,得出比例式求出F的坐标,用待定系数法即可求出抛物线的解析式;
(3)由直角三角形斜边上的中线性质得出MF=![]() CD=
CD=![]() EA,点P与点F重合,得出点P的坐标;由抛物线的对称性得另一点P的坐标即可.
EA,点P与点F重合,得出点P的坐标;由抛物线的对称性得另一点P的坐标即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,Rt△OA1C1 , Rt△OA2C2 , Rt△OA3C3 , Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2 , OA2=OC3 , OA3=OC4…,则依次规律,点A2016的纵坐标为( )
A.0
B.﹣3×( ![]() )2015
)2015
C.(2 ![]() )2016
)2016
D.3×( ![]() )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向ABCD内部投掷飞镖(每次均落在ABCD内,且落在ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() , 连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
, 连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+m与抛物线x2=4y相切,且与x轴的交点为M,点N(﹣1,0).若动点P与两定点M,N所构成三角形的周长为6.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ) 设斜率为 ![]() 的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN.
的直线l交曲线C于A,B两点,当PN⊥MN时,证明:∠APN=∠BPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 ![]() ,则f(x)在[0,k]的最大值h(k)=( )
,则f(x)在[0,k]的最大值h(k)=( )
A.2ln2﹣2﹣(ln2)3
B.﹣1
C.2ln2﹣2﹣(ln2)2k
D.(k﹣1)ek﹣k3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com