Question

【题目】在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．若直线l的极坐标方程为 ，曲线C的极坐标方程为：ρsin2θ=cosθ，将曲线C上所有点的横坐标缩短为原来的一半，纵坐标不变，然后再向右平移一个单位得到曲线C1 ． （Ⅰ）求曲线C1的直角坐标方程；
（Ⅱ）已知直线l与曲线C1交于A，B两点，点P（2，0），求|PA|+|PB|的值．

Answer 1

【答案】解：（I）曲线C的极坐标方程为：ρsin2θ=cosθ，即ρ2sin2θ=ρcosθ，化为直角坐标方程：y2=x． 将曲线C上所有点的横坐标缩短为原来的一半，纵坐标不变，然后再向右平移一个单位得到曲线C1：y2=2（x﹣1）．
（II）直线l的极坐标方程为 ，展开可得： ρ（cosθ+sinθ）﹣2=0，可得直角坐标方程：x+y﹣2=0．
可得参数方程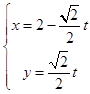： （t为参数）．
代入曲线C1的直角坐标方程可得：t2+2 t﹣4=0．
解得t1+t2=﹣2 ，t1t2=﹣4．．
∴|PA|+|PB|=|t1﹣t2|= = = ．
【解析】（I）曲线C的极坐标方程为：ρsin2θ=cosθ，即ρ2sin2θ=ρcosθ，化为直角坐标方程：y2=x，通过变换可得曲线C1的方程． （II）直线l的极坐标方程为 ，展开可得： ρ（cosθ+sinθ）﹣2=0，利用互化公式可得直角坐标方程．可得参数方程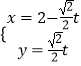： （t为参数），代入曲线C1的直角坐标方程可得：t2+2 t﹣4=0，利用|PA|+|PB|=|t1﹣t2|= 即可得出．