
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}前n项和Tn .
,求数列{bn}前n项和Tn .
【答案】解:(I)∵Sn=2an﹣2,∴n≥2时,an=Sn﹣Sn﹣1=2an﹣2﹣(2an﹣1﹣2),化为:an=2an﹣1 . n=1时,a1=2a1﹣2,解得a1=2.
∴数列{an}是等比数列,首项与公比都为2.
∴an=2n .
(II)bn= ![]() =
= ![]() ,
,
∴数列{bn}前n项和Tn= ![]() +…+
+…+ ![]() ,
,![]() =
= ![]() +…+
+…+ ![]() +
+ ![]() ,
,
∴ ![]() =1+
=1+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =1+
=1+ 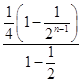 ﹣
﹣ ![]() .
.
∴Tn=3﹣ ![]() .
.
【解析】(I)Sn=2an﹣2,可得n≥2时,an=Sn﹣Sn﹣1 , 化为:an=2an﹣1 . n=1时,a1=2a1﹣2,解得a1 . 利用等比数列的通项公式即可得出.(II)bn= ![]() =
= ![]() ,利用错位相减法与等比数列的求和公式即可得出.
,利用错位相减法与等比数列的求和公式即可得出.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:
【题目】如图,过原点O的直线AB与反比例函数![]() (k>0)的图象交于A、B两点,点B坐标为(﹣2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为.
(k>0)的图象交于A、B两点,点B坐标为(﹣2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F.
(1)求证:EF与⊙O相切;
(2)若AB=6,AD=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为 ![]() ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y2=4x的焦点为F,准线为l.⊙F与C交于A,B两点,与x轴的负半轴交于点P. (Ⅰ)若⊙F被l所截得的弦长为 ![]() ,求|AB|;
,求|AB|;
(Ⅱ)判断直线PA与C的交点个数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF. 
(1)如果 ![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com