
����Ŀ����֪����ABC��ƽ��ֱ������ϵ�е�λ����ͼ����ʾ��A������Ϊ����6��0����B������Ϊ��4��0������DΪBC���е㣬��EΪ�߶�AB��һ���㣬����DE������A��B��C����������ߵĽ���ʽΪy=ax2+bx+8��
��1���������ߵĽ���ʽ��
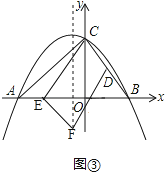
��2����ͼ�٣�����BDE��DEΪ�ᷭ�ۣ���B�ĶԳƵ�Ϊ��G������Gǡ�����������ߵĶԳ�����ʱ����G������ꣻ
��3����ͼ�ڣ�����E���߶�AB���˶�ʱ��������y=ax2+bx+8�ĶԳ������Ƿ���ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������y=ax2+bx+8������A����6��0����B��4��0����
��![]()
���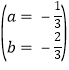
�������ߵĽ���ʽ�ǣ�y=![]() x2��
x2��![]() x+8��
x+8��
��2��
�⣺��ͼ�٣���DM�������ߵĶԳ����ڵ�M��
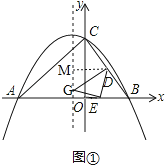
��G�����������1��n����
�ɷ��۵����ʣ��ɵ�BD=DG��
��B��4��0����C��0��8������DΪBC���е㣬
���D�������ǣ�2��4����
���M�������ǣ���1��4����DM=2������1��=3��
��B��4��0����C��0��8����
��BC=![]() =
=![]() ��
��
��![]() ��
��
��Rt��GDM��
32+��4��n��2=20��
���n=4��![]() ��
��
��G�����������1��4+![]() ����1��4��
����1��4��![]() ����
����
��3��
�⣺������y=ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
�ٵ�CD��EF���ҵ�E��x���������ʱ����ͼ�ڣ�
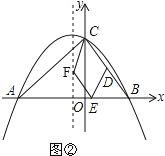
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��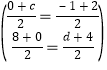
���![]()
���F�������ǣ���1��4������E�������ǣ�1��0����
�ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ����ͼ�ۣ�
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��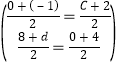
���![]()
���F�������ǣ���1����4������E�������ǣ���3��0����
�۵�CE��DFʱ����ͼ�ܣ�
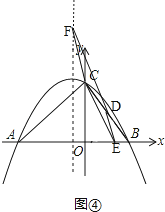 ��
��
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��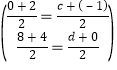
���![]()
���F�������ǣ���1��12������E�������ǣ�3��0����
���ϣ��ɵ�
������y=ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
��F�������ǣ���1��4��������1����4����1��12����
����������1������������y=ax2+bx+8������A����6��0����B��4��0����Ӧ�ô���ϵ��������������ߵĽ���ʽ���ɣ�
��2��������DM�������ߵĶԳ����ڵ�M����G�������Ϊ����1��n�������ݷ��۵����ʣ��ɵ�BD=DG��Ȼ��ֱ������D����M��������Ƕ��٣��Լ�BC��BD��ֵ���Ƕ��٣������Rt��GDM�У����ݹ��ɶ��������n��ֵ���������G������꣮
��3���������⣬������������ٵ�CD��EF���ҵ�E��x���������ʱ���ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ���۵�CE��DFʱ��Ȼ�����ƽ���ı��ε����ʣ������F��������Ƕ��ټ��ɣ�


 ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ������ijУ���ĻС�����óO���ʽ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪B��ѧϰ��Ʒ�ĵ��۱�A��ѧϰ��Ʒ�ĵ��۶�10Ԫ����180Ԫ����B��ѧϰ��Ʒ�ļ�������120Ԫ����A��ѧϰ��Ʒ�ļ�����ͬ��
��1����A��B����ѧϰ��Ʒ�ĵ��۸��Ƕ���Ԫ��
��2������������ѧϰ��Ʒ�ķ��ò�����28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+2������A����1��0���͵�B��4��0��������y�ύ�ڵ�C����D������Ϊ��2��0������P��m��n���Ǹ��������ϵ�һ�����㣬����CA��CD��PD��PB��
��1����������ߵĽ���ʽ��
��2������PDB��������ڡ�CAD�����ʱ�����P�����ꣻ
��3����m��0��n��0ʱ������P��ֱ��PE��y���ڵ�E��ֱ��BC�ڵ�F������F��FG��x���ڵ�G������EG����ֱ��д�����ŵ�P���˶����߶�EG����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��������ABCD�ڵ�һ�㣬����CP�����߶�CP�Ƶ�C˳ʱ����ת90�㣬�õ��߶�CQ������BP��DQ��
��1����ͼa����֤����BCP�ա�DCQ��
��2����ͼ���ӳ�BP��ֱ��DQ�ڵ�E��
����ͼb����֤��BE��DQ��
����ͼc������BCPΪ�ȱ������Σ��жϡ�DEP����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��֯ѧ��ȥ����Ժο�ʣ�������Ʒʱ���֣�����1������Ʒ�ȹ���1������Ʒ�40Ԫ�����һ���600Ԫ�������Ʒ�ͻ���360Ԫ��������Ʒ��������ȣ�
��1����ס���������Ʒ�ĵ��۸�Ϊ����Ԫ��
��2��ѧУ������ס���������Ʒ��30��������Ժ�����ˣ�Ҫ������Ʒ���ܷ��ò�����2000Ԫ����ô���ɹ�����ٸ�����Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽ��е����г��������г���·��Ϊ180ǧ�ף�������ͨ�г���·��Ϊ240ǧ�ף������г���ƽ���ٶ�����ͨ�г���ƽ���ٶȵ�3���������г��ij˳�ʱ�����ͨ�г��ij˳�ʱ��������2Сʱ�������г���ƽ���ٶ���ÿСʱ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���������A����ö���¥BC�Ķ���B������Ϊ32�㣬�ײ�C�ĸ���Ϊ45�㣬�۲����¥��ˮƽ����ADΪ31m����¥BC�ĸ߶�ԼΪ m�����ȡ�����������ο����ݣ�sin32���0.5��cos32���0.8��tan32���0.6��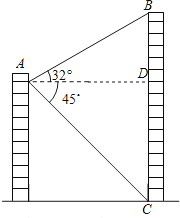
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ2������â�ǡ���������ȫ������������ɣ������غ��ڵ�O������Ա߷ֱ�ƽ�У���A��B�ǡ���â�ǡ�����ͼ1�����������㣬����P�ڡ���â�ǡ��ϣ��ڲ��Լ��߽磩���� ![]() ����x+y��ȡֵ��Χ�ǣ� ��
����x+y��ȡֵ��Χ�ǣ� �� 
A.[��4��4]
B.![]()
C.[��5��5]
D.[��6��6]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У�AB=5������BD��sin��ABD= ![]() ����P������BC�ϵ�һ�����㣨��P�����B�غϣ�������AP����Խ���BD�ཻ�ڵ�E������EC��
����P������BC�ϵ�һ�����㣨��P�����B�غϣ�������AP����Խ���BD�ཻ�ڵ�E������EC��
��1����֤��AE=CE��
��2������P���߶�BC��ʱ����BP=x����PEC�����Ϊy����y����x�ĺ�������ʽ����д�����Ķ�����
��3������P���߶�BC���ӳ�����ʱ������PEC��ֱ�������Σ����߶�BP�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com