Question

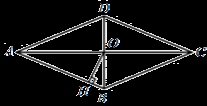
如图，在平行四边形ABCD中，∠DAB=60°，AB=2AD，点 E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G．
（1）求证：四边形DEBF是菱形；
（2）请判断四边形AGBD是什么特殊四边形？并加以证明．

 

 

Answer 1

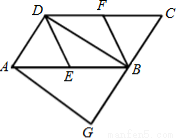
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD且AB=CD，AD∥BC且AD=BC．
E，F分别为AB，CD的中点，
∴BE=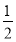AB，DF=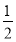CD，
∴BE=BF，
∴四边形DEBF是平行四边形
在△ABD中，E是AB的中点，
∴AE=BE=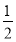AB=AD，
而∠DAB=60°，
∴△AED是等边三角形，即DE=AE=AD，
故DE=BE．
∴平行四边形DEBF是菱形．
（2）【解析】
四边形AGBD是矩形，理由如下：
∵AD∥BC且AG∥DB，
∴四边形AGBD是平行四边形．
由（1）的证明知AD=DE=AE=BE，
∴∠ADE=∠DEA=60°，
∠EDB=∠DBE=30°．
故∠ADB=90°．
∴平行四边形AGBD是矩形．

 

【解析】

（1）利用平行四边形的性质证得△AED是等边三角形，从而证得DE=BE，问题得证；
（2）利用平行四边形的性质证得∠ADB=90°，利用有一个角是直角的平行四边形是矩形判定矩形．