【题目】如图，在平行四边形ABCD中，CE平分∠BCD与AB交于点E，BF平分∠ABC与AD交于点F，若
，EF=4，则CD长为________．
【答案】7
【解析】
已知ABCD是平行四边形，可得∠AFB=∠FBC，BF平分∠ABC，根据角平分线性质定理可得∠ABF=∠FBC，即可得出∠AFB=∠ABF，AB=AF，同理可得∠DEC=∠DCE，ED=CD
设AB=CD=x，AD=10，EF=4，则FD =10-x，ED=14-x，根据ED=CD，可得14-x=x，即可求出x值．
∵ABCD是平行四边形
∴AD∥BC
∴∠AFB=∠FBC
∵BF平分∠ABC
∴∠ABF=∠FBC
∴∠AFB=∠ABF
∴AB=AF
∵AD∥BC
∴∠DEC=∠ECB
∵CE平分∠BCD
∴∠DCE=∠ECB
∴∠DEC=∠DCE
∴ED=CD
设AB=CD=x，AD=10，EF=4
则FD=AD-AF=AD-AB=10-x
∴ED=EF+FD=4+10-x=14-x
∴14-x=x
解得x=7
故答案为：7
科目：初中数学 来源： 题型：
【题目】先化简，再求值： 
÷（
-a+2），其中a=2sin60°+3tan45°．
【答案】﹣
.
【解析】试题分析：先因式分解，再通分，约分化简，代入数值求值.
试题解析：
解：原式= 
÷（
-
）
=
÷
=
，
∵a=2sin60°+3tan45°=2×
+3×1=
+3
∴原式=
=﹣
.
点睛：辨析分式与分式方程
分式，整式A除以整式B,可以表示成的
的形式.如果B中含有字母,那么称 
为分式.分式特点是没有等号，分式加减一般需要通分.
（2）分式方程，分母中含有未知数的方程叫做分式方程.特点是有等号，要先确定最简公分母，去分母的时候要每一项乘以最简公分母，所以一般不需要通分，而且要检验.
【题型】解答题
【结束】
22
【题目】图1，图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．
（1）如图1，在小正方形的顶点上确定一点C，连接AC、BC，使得△ABC为直角三角形，其面积为5，并直接写出△ABC的周长；
（2）如图2，在小正方形的顶点上确定一点D，连接AD、BD，使得△ABD中有一个内角为45°，且面积为3．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（ ）
A. 2
B. 8 C. 2
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为宣传6月6日世界海洋日，某校八年级举行了主题为“珍惜海洋资源，保护海洋生物多样性”的知识竞赛活动．为了解全年级500名学生此次竞赛成绩(百分制)的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表(表1)和统计图(如图)．请根据图表信息解答以下问题：
（1）本次调查一共随机抽取了个参赛学生的成绩；
（2）表1中a＝ ；
（3）所抽取的参赛学生的成绩的中位数落在的“组别”是 ；
（4）请你估计，该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
(1)如图
，已知格点(小正方形的顶点)：
、
、
，若
为格点，请直接画出所有以
、
为勾股边且对角线相等的勾股四边形
；
(2)如图
，将
绕顶点
按顺时针方向旋转
，得到
，连结
、
，
，求证：
，即四边形
是勾股四边形；
(3)如图
，在四边形中，
为等边三角形，
，
，
，求
长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=6，BC=8，E为AB上一点，且AE=2，M为AD上一动点（不与A、D重合），AM=x，连结EM并延长交CD的延长线于F，过M作MG⊥EF交直线BC于点G，连结EG、FG．
（1）如图1，若M是AD的中点，求证：①△AEM≌△DFM；②△EFG是等腰三角形；
（2）如图2，当x为何值时，点G与点C重合？
（3）当x=3时，求△EFG的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，过点A（2，0）的直线l与y轴交于点B，tan∠OAB=
，直线l上的点P位于y轴左侧，且到y轴的距离为1．
（1）求直线l的表达式；
（2）若反比例函数
的图象经过点P，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD∥EF，CD交AF于G，
（1）如图1，若CF平分∠AFE，∠A=70°，求∠C；
（2）如图2，请写出∠A，∠C和∠AFC的数量关系并说明理由.
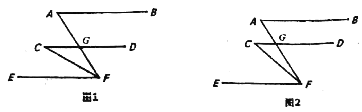
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点．
（1）求证：四边形AMCN是平行四边形；
（2）当AC、BC满足怎样的数量关系时，四边形AMCN是矩形，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com